摘要:将图1中矩形ABCD沿对角线AC剪开.再把△ABC沿着AD方向平移.得到图2中的△A’B’C’,除△ADC与△C’BA’全等外.你还可以指出哪几对全等的三角形?请选择其中一对加以证明.
网址:http://m.1010jiajiao.com/timu_id_745264[举报]
(本小题满分12分)
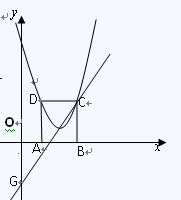
如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=![]() ,直线y=
,直线y=![]() 经过点C,交y轴于点G。
经过点C,交y轴于点G。
1.(1)点C、D的坐标分别是C( ),D( );
2.(2)求顶点在直线y=![]() 上且经过点C、D的抛物
上且经过点C、D的抛物
线的解析式;
3.(3)将(2)中的抛物线沿直线y= 平移,平移后
平移,平移后
的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。
平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?
若存在,请求出此时抛物线的解析式;若不存在,请说
明理由。
查看习题详情和答案>>
(本小题满分12分)
如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC= ,直线y=
,直线y= 经过点C,交y轴于点G。
经过点C,交y轴于点G。

【小题1】(1)点C、D的坐标分别是C( ),D( );
【小题2】(2)求顶点在直线y= 上且经过点C、D的抛物
上且经过点C、D的抛物
线的解析式;
【小题3】(3)将(2)中的抛物线沿直线y= 平移,平移后
平移,平移后
的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。
平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?
若存在,请求出此时抛物线的解析式;若不存在,请说
明理由。 查看习题详情和答案>>
如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=
 ,直线y=
,直线y= 经过点C,交y轴于点G。
经过点C,交y轴于点G。
【小题1】(1)点C、D的坐标分别是C( ),D( );
【小题2】(2)求顶点在直线y=
 上且经过点C、D的抛物
上且经过点C、D的抛物线的解析式;
【小题3】(3)将(2)中的抛物线沿直线y=
 平移,平移后
平移,平移后 的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。
平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?
若存在,请求出此时抛物线的解析式;若不存在,请说
明理由。 查看习题详情和答案>>
(本小题满分12分)
如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC= ,直线y=
,直线y= 经过点C,交y轴于点G。
经过点C,交y轴于点G。

(1)点C、D的坐标分别是C( ),D( );
(2)求顶点在直线y= 上且经过点C、D的抛物
上且经过点C、D的抛物
线的解析式;
(3)将(2)中的抛物线沿直线y= 平移,平移后
平移,平移后
的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。
平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?
若存在,请求出此时抛物线的解析式;若不存在,请说
明理由。 查看习题详情和答案>>
如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=
 ,直线y=
,直线y= 经过点C,交y轴于点G。
经过点C,交y轴于点G。
(1)点C、D的坐标分别是C( ),D( );
(2)求顶点在直线y=
 上且经过点C、D的抛物
上且经过点C、D的抛物线的解析式;
(3)将(2)中的抛物线沿直线y=
 平移,平移后
平移,平移后 的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。
平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?
若存在,请求出此时抛物线的解析式;若不存在,请说
明理由。 查看习题详情和答案>>
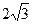 ,直线y=
,直线y=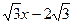 经过点C,交y轴于点G。
经过点C,交y轴于点G。
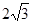 ,直线y=
,直线y=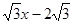 经过点C,交y轴于点G。
经过点C,交y轴于点G。