摘要:对于实数a, b, c, d规定一种运算:.如.那么时.x=
网址:http://m.1010jiajiao.com/timu_id_745242[举报]
对于实数a,b,c,d规定一种运算:
=ad-bc,如
=1×(-2)-0×2=-2,那么
=25时,x=( )
|
|
|
A、-
| ||
B、
| ||
C、-
| ||
D、-
|
在数学里,我们规定:a-n=
(a≠O).无论从仿照同底数幂的除法公式来分析,还是仿照分式的约分来分析,这种规定都是合理的.正是有了这种规定,指数的范围由非负数扩大到全体整数,概念的扩充与完善使我们解决问题的路更宽了.例如a2•a-3=a2+(-3)=a-1=
.数的发展经历了漫长的过程,其实人们早就发现了非实数的数.人们规定:i2=-1,这里数i类似于实数单位1,它的运算法则与实数运算法则完全类似:2i+
i=
i(注意:由于非实数与实数单位不同,因此像2+i之类的运算便无法继续进行,2+i就是一个非实数的数),6•0.5i=3i; 2i•3i=6i2=-6;(3i)2=-9;-4的平方根为±2i;如果x2=-7,那么x=±
i.…数的不断发展进一步证实,这种规定是合理的.
(1)想一想,作这样的规定有什么好处?
(2)试用配方法求一元二次方程x2+x+1=0的非实数解:
(3)你认为,在学习中,当面临一个新的挑战时,我们应如何面对?
查看习题详情和答案>>
| 1 |
| an |
| 1 |
| a |
| 1 |
| 3 |
| 7 |
| 3 |
| 7 |
(1)想一想,作这样的规定有什么好处?
(2)试用配方法求一元二次方程x2+x+1=0的非实数解:
(3)你认为,在学习中,当面临一个新的挑战时,我们应如何面对?
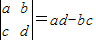 ,如
,如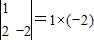 -0×2=-2,那么
-0×2=-2,那么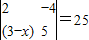 时,x=( )
时,x=( )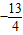
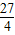
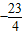
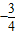
 ,如
,如 ,那么当
,那么当 时,则
时,则 =( )
=( )