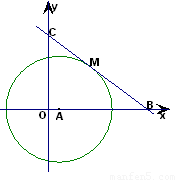
摘要：23． 如图(7)点A.B.D.E在⊙O上.AE.BD的廷长线交于C.给出下列三个条件:①AB是⊙O的直径,②D是BC的中点,③∠B=∠C．请在上述条件中任意选取两个作为已知条件.第三个作为结论.写出一个你认为正确的命题.并加以证明．
网址：http://m.1010jiajiao.com/timu_id_742396[举报]
(本题8分)如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，10为半径作⊙O，分别与∠EPF的两边相交于A、B和C、D，连结OA，此时有OA//PE．
（1）求证：AP=AO；
（2）若tan∠OPB=
，求弦AB的长；
（3）若以图中已标明的点（即P、A、B、C、D、O）构造四边形，则能构成菱形的四个点为 ▲ ，能构成等腰梯形的四个点为 ▲ 或 ▲ 或 ▲ .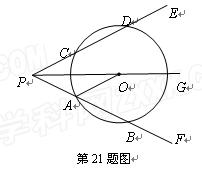
查看习题详情和答案>>
（1）求证：AP=AO；
（2）若tan∠OPB=
，求弦AB的长；（3）若以图中已标明的点（即P、A、B、C、D、O）构造四边形，则能构成菱形的四个点为 ▲ ，能构成等腰梯形的四个点为 ▲ 或 ▲ 或 ▲ .
查看习题详情和答案>>
(本题12分) 如图，在平面直角坐标系中，二次函数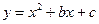
的图象与x轴交于A、B两点， A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，-3）点，点P是直线BC下方的抛物线上一动点.
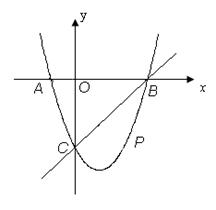
（1）求b,c的值．
（2）连结PO、PC，并把△POC沿CO翻折，得到四边形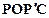
， 那么是否存在点P，使四边形
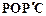为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．
（3）当点P运动到什么位置时，四边形 ABPC的面积最大，并求出此时P点的坐标和四边形ABPC的最大面积. 查看习题详情和答案>>
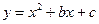的图象与x轴交于A、B两点， A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，-3）点，点P是直线BC下方的抛物线上一动点.（1）求b,c的值．
（2）连结PO、PC，并把△POC沿CO翻折，得到四边形
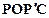， 那么是否存在点P，使四边形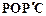为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．（3）当点P运动到什么位置时，四边形 ABPC的面积最大，并求出此时P点的坐标和四边形ABPC的最大面积. 查看习题详情和答案>>
若点M(m，1)是抛物线上对称轴右侧的一点，点Q也在抛物线上，点P在x轴上，是否存在以O、M、P、Q为顶点的四边形是平行四边形，若存在，请直接写出点P的坐标；若不存在，请说明理由．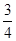
x+b过点M，分别交x轴、y轴于B、C两点．