网址：http://m.1010jiajiao.com/timu_id_739472[举报]
文天祥字宋瑞，又字履善，吉之吉水人也。年二十举进士，对策集英殿。帝亲拔为第一。咸淳九年，起为湖南提刑，因见故相江万里。万里素奇天祥志节，语及国事，愀然曰：“吾老矣，观天时人事当有变，吾阅人多矣，世道之责，其在君乎?君其勉之。”十年，改知赣州。德祐初，江上报急，诏天下勤王。天祥捧诏涕泣，发郡中豪杰，有众万人。事闻，以江西提刑安抚使召入卫。其友止之，天祥曰：“第国家养育臣庶三百余年，一旦有急，征天下兵，无一人一骑入关者，吾深恨于此，故不自量力，而以身徇之，庶天下忠臣义士将有闻风而起者。”尽以家赀为军费。明年正月，除知临安府，寻除右丞相兼枢密使，如军中请和，与大元丞相伯颜抗论皋亭山。丞相怒拘之，北至镇江。天祥夜亡入真州，展转至高邮，泛海至温州。至元十五年十二月，趋南岭。天祥方饭五坡岭，张弘范兵突至，天祥仓皇出走，千户王惟义前执之。至潮阳，见弘范，左右命之拜，不拜，弘范遂以客礼见之，与俱入崖山，使为书招张世杰。天祥曰：“吾不能捍父母，乃教人叛父母，可乎?”索之固，乃书所过零丁洋诗与之。崖山破，弘范遣使护送天祥至京师。天祥在燕凡三年，上知天祥终不屈也，召入谕之曰：“汝何愿?”天祥对曰：“天祥受宋恩，为宰相，安事二姓?愿赐之一死足矣。”然犹不忍，遽麾之退。言者力赞从天祥之请，从之。天祥临刑殊从容。谓吏卒曰：“吾事毕矣。”南乡拜而死，年四十七。 (节选自《宋史·文天祥传》)
【小题1】对下列句中加点的词语的解释，不正确的一项是
| A．年二十举进士，对策集英殿对策：对付的策略 |
| B．第国家养育臣庶三百余年 养育：养活、抚养 |
| C．吾深恨于此深恨：非常遗憾 |
| D．天祥临刑殊从容 从容：沉着镇静 |
①捧诏涕泣 ②与大元丞相伯颜抗论皋亭山 ③尽以家赀为军费 ④左右命之拜，不拜 ⑤张弘范兵突至，天祥仓皇出走 ⑥天祥受宋恩，为宰相，安事二姓?
| A．①③④ | B．②④⑥ | C．①⑤⑥ | D．②③⑤ |
| A．咸淳九年，文天祥任湖南提刑时遇见旧相江万里，谈及国家大事，江万里容色改变，认为改变社会状况的责任大概在有志节的文天祥身上。 |
| B．德祐元年，元军进逼愈急，皇上下诏号召天下起兵帮助朝廷抗敌，文天祥“发郡中豪杰”响应，有众万人，并倾尽家财为军费，领兵入卫。 |
| C．德祐二年，文天祥奉命赴元朝都城跟元丞相伯颜谈判时据理力争，遭到元方的扣押，被带到镇江，后来趁夜色逃离，最后来到温州。 |
| D．至元十五年，元将张弘范兵突至，文天祥在五坡岭被执。崖山被攻破后，文天祥被送往京师。元朝百般劝降，他坚决不屈服，最后从容就义。 |
(1)庶天下忠臣义士将有闻风而起者。（5分）
翻译：
(2)左右命之拜，不拜，弘范遂以客礼见之。（5分）
翻译： 查看习题详情和答案>>
下列说法正确的是（??? ）
A．一颗质地均匀的骰子已连续抛掷了2000次，其中，抛掷出5点的次数最少，则第2001次一定抛掷出5点。
B．某种彩票中奖的概率是1%，因此买100张该种彩票一定会中奖。
C．天气预报说明天下雨的概率是50%，所以明天将有一半时间在下雨。
D．抛掷一枚图钉，钉尖触地和钉尖朝上的概率不相等。
查看习题详情和答案>>
| A．一颗质地均匀的骰子已连续抛掷了2000次，其中，抛掷出5点的次数最少，则第2001次一定抛掷出5点。 |
| B．某种彩票中奖的概率是1%，因此买100张该种彩票一定会中奖。 |
| C．天气预报说明天下雨的概率是50%，所以明天将有一半时间在下雨。 |
| D．抛掷一枚图钉，钉尖触地和钉尖朝上的概率不相等。 |
阅读材料：（本题8分）
例：说明代数式 
的几何意义，并求它的最小值．
解： 
，如图，建立平面直角坐标系，点P（x，0）是x轴上一点，则
可以看成点P与点A（0，1）的距离，
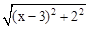可以看成点P与点B（3，2）的距离，所以原代数式的值可以看成线段PA与PB长度之和，它的最小值就是PA＋PB的最小值．
设点A关于x轴的对称点为A′，则PA＝PA′，因此，求PA＋PB的最小值，
只需求PA′＋PB的最小值，而点A′、B间的直线段距离最短，
所以PA′＋PB的最小值为线段A′B的长度．为此，构造直角
三角形A′CB，因为A′C＝3，CB＝3，所以A′B＝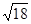
，
即原式的最小值为。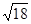
根据以上阅读材料，解答下列问题：
（1）代数式
的值可以看成平面直角坐标系中点P（x，0）与点A（1，1）、点B 的距离之和．（填写点B的坐标）
（2）求代数式 
的最小值
阅读材料：（本题8分）
例：说明代数式 
的几何意义，并求它的最小值．
解： 
，如图，建立平面直角坐标系，点P（x，0）是x轴上一点，则
可以看成点P与点A（0，1）的距离，
可以看成点P与点B（3，2）的距离，所以原代数式的值可以看成线段PA与PB长度之和，它的最小值就是PA＋PB的最小值．
设点A关于x轴的对称点为A′，则PA＝PA′，因此，求PA＋PB的最小值，
只需求PA′＋PB的最小值，而点A′、B间的直线段距离最短，
所以PA′＋PB的最小值为线段A′B的长度．为此，构造直角
三角形A′CB，因为A′C＝3，CB＝3，所以A′B＝
，
即原式的最小值为。
根据以上阅读材料，解答下列问题：
（1）代数式
的值可以看成平面直角坐标系中点P（x，0）与点A（1，1）、点B 的距离之和．（填写点B的坐标）
（2）求代数式 
的最小值
查看习题详情和答案>>