摘要：11．如图.直线AB.CD相交于点O.因为Ðl+Ð3=180°.Ð2+ Ð3=180°.所以Ðl=Ð2.其推理的依据是 .
网址：http://m.1010jiajiao.com/timu_id_737550[举报]
如图，直线AB、CD相交于点O，因为∠1+∠3=180°.∠2+∠3=180°，所以∠1=∠2，它的推理依据是( ).
A
.同角的余角相等 B.等角的余角相等C.
同角的补角相等 D.等角的补角相等
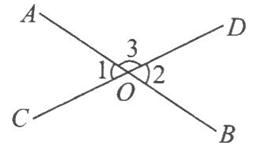
图3,直线AB与CD相交于点O,OP是∠BOC的平分线，OE⊥AB，OF⊥CD.
（1）写出图中(除直角相等外)两对相等的角：________与________、_______与________
（2）如果∠AOD＝40°．
①那么根据 ，可得∠BOC＝ 度．
②因为OP是∠BOC的平分线，所以∠COP=
∠ = 度.
③∠BOF=_____度．
如图，直线AB、CD交于点O，因为∠1＋∠3=180°，∠2＋∠3=180°，所以∠1=∠2，它的理论依据是
[ ]
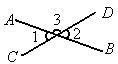
A．同角的余角相等
B．等角的余角相等
C．同角的补角相等
D．等角的补角相等
如图，直线AB、CD交于点O，OE⊥AB，0为垂足，∠AOC=60°，求∠DOE的度数．（填空并添写理由）解：因为AB、CD交于O点，∠AOC=60°（已知）
所以∠BOD=∠AOC=
60
60
度 （对顶角相等
对顶角相等
）因为OE⊥AB （
已知
已知
）所以∠BOE=
90
90
度 （垂直的定义
垂直的定义
）所以∠EOD=∠BOE-∠BOD=
30
30
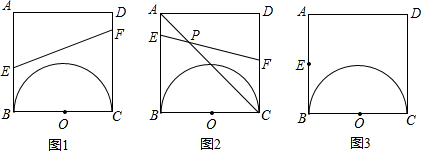
度．如图1，正方形ABCD中，有一直径为BC=2cm 的半圆O．两点E、F分别从点B、点A同时出发，点E沿线段BA以1cm/s的速度向点A运动，点F沿折线A-D-C以2cm/s的速度向点C运动．设点E离开点的B时间为t（s），其中1≤t＜2．
（1）当t为何值时，线段EF和BC平行？
（2）EF能否与半圆O相切？如果能，求出t的值；如果不能，请说明原因．
（3）如图2，设EF与AC相交于点P，当点E、F运动时，点P的位置是否发生变化？若发生变化，请说明理由；若不发生变化，也请说明理由，并求AP：PC的值．
变式：如图3，若将上题改为，正方形ABCD中，有一直径为BC=2cm的半圆O．点E为AB边上的动点（不与点A、B重合），过点E与圆O相切的直线交CD所在直线为点F，设EB=x，FD=y．
（1）试写出y关于x的函数关系式，并写出自变量x的取值范围．
（2）是否存在切线EF，把正方形ABCD的周长分成相等的两部分？若存在，求出x的值．若不存在，请说明理由．
查看习题详情和答案>>
（1）当t为何值时，线段EF和BC平行？
（2）EF能否与半圆O相切？如果能，求出t的值；如果不能，请说明原因．
（3）如图2，设EF与AC相交于点P，当点E、F运动时，点P的位置是否发生变化？若发生变化，请说明理由；若不发生变化，也请说明理由，并求AP：PC的值．
变式：如图3，若将上题改为，正方形ABCD中，有一直径为BC=2cm的半圆O．点E为AB边上的动点（不与点A、B重合），过点E与圆O相切的直线交CD所在直线为点F，设EB=x，FD=y．
（1）试写出y关于x的函数关系式，并写出自变量x的取值范围．
（2）是否存在切线EF，把正方形ABCD的周长分成相等的两部分？若存在，求出x的值．若不存在，请说明理由．