摘要：(1一)(1++2+3)= (2)观察上式并猜想:
网址：http://m.1010jiajiao.com/timu_id_736033[举报]
观察以下式子：
→
=
＞
，
→
=
＜
，
→
=
＞
，
→
=2＜
．请你猜想，将一个正分数的分子分母同时加上一个正数，这个分数的变化情况，并证明你的结论．
查看习题详情和答案>>
| 1 |
| 2 |
| 1+1 |
| 2+1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 5 |
| 4 |
| 5+2 |
| 4+2 |
| 7 |
| 6 |
| 5 |
| 4 |
| 3 |
| 5 |
| 3+5 |
| 5+5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 7 |
| 2 |
| 7+3 |
| 2+3 |
| 7 |
| 2 |
观察与思考：
①2
=
②3
=
③4
=
式①验证：2
=
=
=
=
式②验证：3
=
=
=
=
（1）仿照上述式①、式②的验证过程，请写出式③的验证过程；
（2）猜想
=
（3）试用含n（n为自然数，且n≥2）的等式表示这一规律，并加以验证． 查看习题详情和答案>>
①2
|
2
|
|
3
|
|
4
|
式①验证：2
|
|
|
|
2
|
式②验证：3
|
|
|
|
3
|
（1）仿照上述式①、式②的验证过程，请写出式③的验证过程；
（2）猜想
5
|
（3）试用含n（n为自然数，且n≥2）的等式表示这一规律，并加以验证． 查看习题详情和答案>>
观察下列等式：
①1-
=
；
②
-
=
；
③
-
=
；
④
-
=
；
…
（1）猜想并写出第n个算式： ；
（2）请说明你写出的等式的正确性；
（3）把上述n个算式的两边分别相加，会得到下面的求和公式吗？请写出具体的推导过程．
+
+
+…+
= ；
（4）我们规定：分子是1，分母是正整数的分数叫做单位分数．任意一个真分数都可以表示成不同的单位分数的和的形式，且有无数多种表示方法．根据上面得出的两个结论，请将真分数
表示成不同的单位分数的和的形式．（写出一种即可）
查看习题详情和答案>>
①1-
| 1 |
| 2 |
| 1 |
| 1×2 |
②
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2×3 |
③
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3×4 |
④
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 4×5 |
…
（1）猜想并写出第n个算式：
（2）请说明你写出的等式的正确性；
（3）把上述n个算式的两边分别相加，会得到下面的求和公式吗？请写出具体的推导过程．
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
（4）我们规定：分子是1，分母是正整数的分数叫做单位分数．任意一个真分数都可以表示成不同的单位分数的和的形式，且有无数多种表示方法．根据上面得出的两个结论，请将真分数
| 2 |
| 3 |
； ②
；
； ④
；
个算式： ；
．
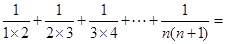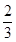表示成不同的单位分数的和的形式．（写出一种即可）