摘要：求证:(1), (2).
网址：http://m.1010jiajiao.com/timu_id_734521[举报]
（1）求证：关于x的一元二次方程x2+（m-3）x-3m=0一定有两个实数根；
（2）若关于x的方程x2-
x+3k-6=0有两个不相等的实数根，求k的取值范围；
（3）设题（1）中方程的两根为a、b，若恰有一个直角三角形的三边长分别为2、a、b，试求m的值。
查看习题详情和答案>>
（2）若关于x的方程x2-
x+3k-6=0有两个不相等的实数根，求k的取值范围；（3）设题（1）中方程的两根为a、b，若恰有一个直角三角形的三边长分别为2、a、b，试求m的值。
如图：在平面直角坐标系中，A（4，0）、B（-1，0）。C以AB的中点P为圆心，AB为直径作⊙P与y轴的正半轴交于点C。
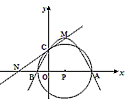
（1） 求经过A、B、C三点的抛物线对应的函数解析式；
（2） 设M为（1）抛物线的顶点，求直线MC对应的函数解析式；
（3） 试说明直线MC与⊙P的位置关系，并证明你的结论。
查看习题详情和答案>>
（2） 设M为（1）抛物线的顶点，求直线MC对应的函数解析式；
（3） 试说明直线MC与⊙P的位置关系，并证明你的结论。
已知：如图，抛物线y=ax2+bx+c经过A（1，0）、B（5，0）、C（0，5）三点。
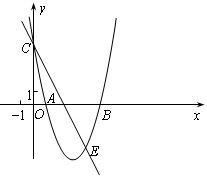
（1）求抛物线的函数关系式；
（2）若过点C的直线y=kx+b与抛物线相交于点E（4，m），请求出△CBE的面积S的值；
（3）在抛物线上求一点P0，使得△ABP0为等腰三角形，并写出P0点的坐标；
（4）除（3）中所求的P0点外，在抛物线上是否还存在其它的点P使得△ABP为等腰三角形？若存在，请求出一共有几个满足条件的点P（要求简要说明理由，但不证明）；若不存在这样的点P，请说明理由。
查看习题详情和答案>>
（2）若过点C的直线y=kx+b与抛物线相交于点E（4，m），请求出△CBE的面积S的值；
（3）在抛物线上求一点P0，使得△ABP0为等腰三角形，并写出P0点的坐标；
（4）除（3）中所求的P0点外，在抛物线上是否还存在其它的点P使得△ABP为等腰三角形？若存在，请求出一共有几个满足条件的点P（要求简要说明理由，但不证明）；若不存在这样的点P，请说明理由。
已知：抛物线y=ax2+bx+c（a≠0），顶点C（1，-4），与x轴交于A、B两点，A（-1，0）。
（1）求这条抛物线的解析式；
（2）如图，以AB为直径作圆，与抛物线交于点D，与抛物线的对称轴交于E，依次连接A、D、B、E，点Q为AB上一个动点（Q与A、B两点不重合），过点Q作QF⊥AE于F，QG⊥DB于G，请判断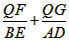
是否为定值，若是，请求出此定值，若不是，请说明理由；
（3）在（2）的条件下，若点H是线段EQ上一点，过点H作MN⊥EQ，MN分别与边AE、BE相交于M、N（M与A、E不重合，N与E、B不重合），请判断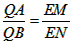
是否成立，若成立，请给出证明，若不成立，请说明理由。
（1）求这条抛物线的解析式；
（2）如图，以AB为直径作圆，与抛物线交于点D，与抛物线的对称轴交于E，依次连接A、D、B、E，点Q为AB上一个动点（Q与A、B两点不重合），过点Q作QF⊥AE于F，QG⊥DB于G，请判断
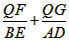是否为定值，若是，请求出此定值，若不是，请说明理由； （3）在（2）的条件下，若点H是线段EQ上一点，过点H作MN⊥EQ，MN分别与边AE、BE相交于M、N（M与A、E不重合，N与E、B不重合），请判断
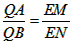是否成立，若成立，请给出证明，若不成立，请说明理由。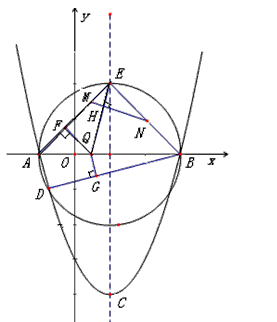
1.背景 ：在图1中，已知线段AB，CD。其中点分别是E，F。
①若A（-1,0），B（3,0），则E点的坐标为________;
②若C（-2,2），D（-2,-1），则F点的坐标为_________;
2.探究： 在图2中，已知线段AB的端点坐标A（a,b）,B(c,d),求出图中AB中点D的坐标（用含a,b,c,d的代数式表示），并给出求解过程；
归纳： 无论线段AB处于直角坐标系中的哪个位置，当其端点坐标为A（a,b）,B(c,d),AB中点为D（x,y）时，x=______,y=_________(不必证明)。
运用： 在图3中，一次函数y=x-2与反比例函数
的图像交点为A，B。
①求出交点A,B的坐标；
②若以A、O、B、P为顶点的四边形是平行四边形，请利用上面的结论求出顶点P的坐标。
查看习题详情和答案>>