摘要：(0.4)．动点M从点O出发.沿OA方向以每秒1个单位长度的速度向终点A运动,同时.动点N从点A出发沿AB方向以每秒个单位长度的速度向终点B运动．设运动了x秒．
网址：http://m.1010jiajiao.com/timu_id_734431[举报]
如图，平面上一点P从点M（
，1）出发，沿射线OM方向以每秒1个单位长度的速度作匀速运动，在运动过程中，以OP为对角线的矩形OAPB的边长OA：OB=1：
；过点O且垂直于射线OM的直线l与点P同时出发，且与点P沿相同的方向、以相同的速度运动．
（1）在点P运动过程中，试判断AB与y轴的位置关系，并说明理由．
（2）设点P与直线l都运动了t秒，求此时的矩形OAPB与直线l在运动过程中所扫过的区域的重叠部分的面积S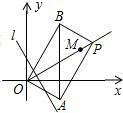
．（用含t的代数式表示）
查看习题详情和答案>>
| 3 |
| 3 |
（1）在点P运动过程中，试判断AB与y轴的位置关系，并说明理由．
（2）设点P与直线l都运动了t秒，求此时的矩形OAPB与直线l在运动过程中所扫过的区域的重叠部分的面积S
．（用含t的代数式表示）
查看习题详情和答案>>
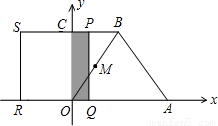
如图，梯形OABC中，CB∥OA，O为坐标原点，A（4，0），C（0，4），tan∠BAO=2，动点P从点C出发，以每秒1个单位的速度沿线段CB运动到点B后，再以每秒
个单位的速度沿线段BA运动，到点A停止，过点P作PQ⊥x轴于Q，以PQ为一边向左作
正方形PQRS，设运动时间为t（秒），正方形PQRS与梯形ABCD重叠的面积为S（平方单位）．
（1）求点B的坐标．
（2）求S与t的函数关系式．
（3）求（2）中的S的最大值．
（4）连接OB，OB中点为M，正方形PQRS在变化过程中，使点M在正方形PQRS的边上的t值为
查看习题详情和答案>>
| 5 |
正方形PQRS，设运动时间为t（秒），正方形PQRS与梯形ABCD重叠的面积为S（平方单位）．（1）求点B的坐标．
（2）求S与t的函数关系式．
（3）求（2）中的S的最大值．
（4）连接OB，OB中点为M，正方形PQRS在变化过程中，使点M在正方形PQRS的边上的t值为
1秒或3秒
1秒或3秒
．
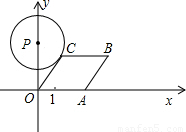
如图所示，已知A点从（1，0）点出发，以每秒1个单位长的速度沿着x轴的正方向运动，经过t秒后，以O、A为顶点作菱形OABC，使B、C点都在第一象限内，且∠AOC=60°，又以P（0，4）为圆心，PC为半径的圆恰好与OA所在的直线相切，则t= ．
查看习题详情和答案>>
查看习题详情和答案>>
个单位的速度沿线段BA运动，到点A停止，过点P作PQ⊥x轴于Q，以PQ为一边向左作正方形PQRS，设运动时间为t（秒），正方形PQRS与梯形ABCD重叠的面积为S（平方单位）．