摘要：4．如图.点A的坐标为(1.0).点B在直线上运动.当线段AB最短时.点B的坐标为
网址：http://m.1010jiajiao.com/timu_id_727156[举报]
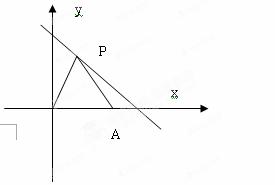
如图，点A坐标为（4,0），点P在第一象限且在直线
y=－x+5上
（1） 设点P坐标为（x,y），写出ΔOPA的面积S与x之间的关系式（其中点P横坐标在O与A点之间变化）
（2） 当S=12时，求点P的坐标
（3） 若ΔOPA是直角三角形，求P点坐标，并求面积
如图，点A在x轴的负半轴上，OA=4，AB=OB=
．将△ABO绕坐标原点O顺时针旋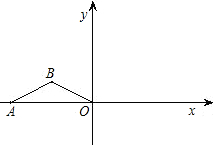
转90°，得到△A1B1O，再继续旋转90°，得到△A2B2O．抛物线y=ax2+bx+3经过B、B1两点．
（1）求抛物线的解析式；
（2）点B2是否在此抛物线上，请说明理由；
（3）在该抛物线上找一点P，使得△PBB2是以BB2为底的等腰三角形，求出所有符合条件的点P的坐标；
（4）在该抛物线上，是否存在两点M、N，使得原点O是线段MN的中点？若存在，直接写出这两点的坐标；若不存在，请说明理由． 查看习题详情和答案>>
| 5 |
转90°，得到△A1B1O，再继续旋转90°，得到△A2B2O．抛物线y=ax2+bx+3经过B、B1两点．（1）求抛物线的解析式；
（2）点B2是否在此抛物线上，请说明理由；
（3）在该抛物线上找一点P，使得△PBB2是以BB2为底的等腰三角形，求出所有符合条件的点P的坐标；
（4）在该抛物线上，是否存在两点M、N，使得原点O是线段MN的中点？若存在，直接写出这两点的坐标；若不存在，请说明理由． 查看习题详情和答案>>
如图，点A为x轴负半轴上一点，点B为x轴正半轴上一点，OA，OB（OA＜OB）的长分别是关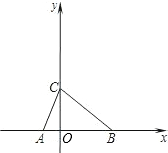
于x的一元二次方程x2-4mx+m2+2=0的两根，C（0，3），且S△ABC=6
（1）求∠ABC的度数；
（2）过点C作CD⊥AC交x轴于点D，求点D的坐标；
（3）在第（2）问的条件下，y轴上是否存在点P，使∠PBA=∠CAB？若存在，请直接写出直线PD的解析式；若不存在，请说明理由． 查看习题详情和答案>>
于x的一元二次方程x2-4mx+m2+2=0的两根，C（0，3），且S△ABC=6（1）求∠ABC的度数；
（2）过点C作CD⊥AC交x轴于点D，求点D的坐标；
（3）在第（2）问的条件下，y轴上是否存在点P，使∠PBA=∠CAB？若存在，请直接写出直线PD的解析式；若不存在，请说明理由． 查看习题详情和答案>>
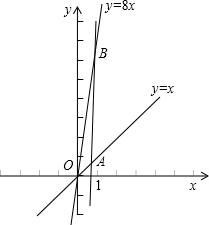如图，点A，B分别在一次函数y=x，y=8x的图象上，其横坐标分别为a，b （a＞0，b＞0 ）．若直线AB为一次函数y=kx+m的图象，则当
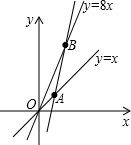如图，点A，B分别在一次函数y=x，y=8x的图象上，其横坐标分别为a，b （a＞0，b＞0）．设直线AB的解析式为y=kx+m，若