摘要:19.用一个三角形.一个长方形和一个圆设计一个轴对称图形.并说明你要表达的含义.
网址:http://m.1010jiajiao.com/timu_id_724905[举报]
(本题满分7分) 和
和 是绕点
是绕点 旋转的两个相似三角形,其中
旋转的两个相似三角形,其中 与
与 、
、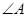 与
与 为对应角.
为对应角.

【小题1】(1)如图1,若 和
和 分别是以
分别是以 与
与 为顶角的等腰直角三角形,且两三角形旋转到使点
为顶角的等腰直角三角形,且两三角形旋转到使点 、
、 、
、 在同一条直线上的位置时,请直接写出线段
在同一条直线上的位置时,请直接写出线段 与线段
与线段 的关系;
的关系;
【小题2】(2)若 和
和 为含有
为含有 角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段
角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段 与线段
与线段 的关系,并说明理由;
的关系,并说明理由;
【小题3】(3)若 和
和 为如图3的两个三角形,且
为如图3的两个三角形,且 =
= ,
, ,在绕点
,在绕点 旋转的过程中,直线
旋转的过程中,直线 与
与 夹角的度数是否改变?若不改变,直接用含
夹角的度数是否改变?若不改变,直接用含 、
、 的式子表示夹角的度数;若改变,请说明理由.
查看习题详情和答案>>
的式子表示夹角的度数;若改变,请说明理由.
查看习题详情和答案>>
 和
和 是绕点
是绕点 旋转的两个相似三角形,其中
旋转的两个相似三角形,其中 与
与 、
、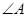 与
与 为对应角.
为对应角.
【小题1】(1)如图1,若
 和
和 分别是以
分别是以 与
与 为顶角的等腰直角三角形,且两三角形旋转到使点
为顶角的等腰直角三角形,且两三角形旋转到使点 、
、 、
、 在同一条直线上的位置时,请直接写出线段
在同一条直线上的位置时,请直接写出线段 与线段
与线段 的关系;
的关系;【小题2】(2)若
 和
和 为含有
为含有 角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段
角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段 与线段
与线段 的关系,并说明理由;
的关系,并说明理由;【小题3】(3)若
 和
和 为如图3的两个三角形,且
为如图3的两个三角形,且 =
= ,
, ,在绕点
,在绕点 旋转的过程中,直线
旋转的过程中,直线 与
与 夹角的度数是否改变?若不改变,直接用含
夹角的度数是否改变?若不改变,直接用含 、
、 的式子表示夹角的度数;若改变,请说明理由.
查看习题详情和答案>>
的式子表示夹角的度数;若改变,请说明理由.
查看习题详情和答案>>
(本小题满分7分)
如图,矩形ABCD,AB=4,AD=3,动点M、N分别从D、B同时出发,以1个
单位/秒的速度运动,点M沿DA向终点A运动,点N沿BC向终点C运动。过点
N作NP⊥BC,交AC于点P,连结MP。已知动点M、N运动了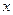 秒.
秒.
⑴请直接写出PN的长;(用含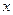 的代数式表示)
的代数式表示)
⑵若0秒≤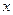 ≤1秒,试求△MPA的面积S与时间
≤1秒,试求△MPA的面积S与时间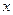 秒的函数关系式,利用函数图
秒的函数关系式,利用函数图
象,求S的最大值;
⑶若0秒≤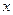 ≤3秒,△MPA能否为一个等腰三角形?若能,试求出所有
≤3秒,△MPA能否为一个等腰三角形?若能,试求出所有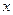 的对应
的对应
值;若不能,试说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
如图,矩形ABCD,AB=4,AD=3,动点M、N分别从D、B同时出发,以1个
单位/秒的速度运动,点M沿DA向终点A运动,点N沿BC向终点C运动。过点
N作NP⊥BC,交AC于点P,连结MP。已知动点M、N运动了
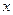 秒.
秒.⑴请直接写出PN的长;(用含
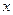 的代数式表示)
的代数式表示)⑵若0秒≤
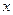 ≤1秒,试求△MPA的面积S与时间
≤1秒,试求△MPA的面积S与时间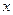 秒的函数关系式,利用函数图
秒的函数关系式,利用函数图象,求S的最大值;
⑶若0秒≤
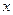 ≤3秒,△MPA能否为一个等腰三角形?若能,试求出所有
≤3秒,△MPA能否为一个等腰三角形?若能,试求出所有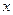 的对应
的对应值;若不能,试说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
(本小题满分7分)
如图,矩形ABCD,AB=4,AD=3,动点M、N分别从D、B同时出发,以1个
单位/秒的速度运动,点M沿DA向终点A运动,点N沿BC向终点C运动。过点
N作NP⊥BC,交AC于点P,连结MP。已知动点M、N运动了 秒.
秒.
⑴请直接写出PN的长;(用含 的代数式表示)
的代数式表示)
⑵若0秒≤ ≤1秒,试求△MPA的面积S与时间
≤1秒,试求△MPA的面积S与时间 秒的函数关系式,利用函数图
秒的函数关系式,利用函数图
象,求S的最大值;
⑶若0秒≤ ≤3秒,△MPA能否为一个等腰三角形?若能,试求出所有
≤3秒,△MPA能否为一个等腰三角形?若能,试求出所有 的对应
的对应
值;若不能,试说明理由.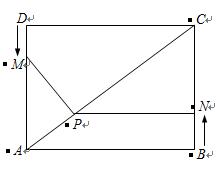
 和
和 是绕点
是绕点 旋转的两个相似三角形,其中
旋转的两个相似三角形,其中 与
与 、
、 与
与 为对应角.
为对应角.
 、
、 在同一条直线上的位置时,请直接写出线段
在同一条直线上的位置时,请直接写出线段 与线段
与线段 的关系;
的关系; 角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段
角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段 =
= ,
, ,在绕点
,在绕点 的式子表示夹角的度数;若改变,请说明理由.
的式子表示夹角的度数;若改变,请说明理由. 秒.
秒.