网址:http://m.1010jiajiao.com/timu_id_72086[举报]
一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
ADBAC BCABC
※1.A (1) .files/image002.gif) 比
比.files/image004.gif) 大,实数与虚数不能比较大小;(2)两个复数互为共轭复数时其和为实数,但是两个复数的和为实数不一定是共轭复数;
大,实数与虚数不能比较大小;(2)两个复数互为共轭复数时其和为实数,但是两个复数的和为实数不一定是共轭复数;
(3).files/image006.gif) 的充要条件为
的充要条件为.files/image008.gif) 是错误的,因为没有表明
是错误的,因为没有表明.files/image148.gif) 是否是实数;
是否是实数;
(4)当.files/image150.gif) 时,没有纯虚数和它对应
时,没有纯虚数和它对应
※2.D .files/image152.gif) ,虚部为
,虚部为.files/image029.gif)
※3.B .files/image155.gif) ;
;.files/image157.gif) ,反之不行,例如
,反之不行,例如.files/image159.gif) ;
;.files/image035.gif) 为实数不能推出
为实数不能推出
.files/image161.gif) ,例如
,例如.files/image163.gif) ;对于任何
;对于任何.files/image069.gif) ,
,.files/image039.gif) 都是实数
都是实数
※4.A .files/image166.gif)
※5.C .files/image168.gif)
※6.B .files/image170.gif)
※7.C
.files/image172.gif) ,
,.files/image174.gif)
※8.A
.files/image176.gif)
※9.B
.files/image178.gif)
※10.C
二、填空题(每小题5分, 4题共20分)。
※11..files/image180.gif)
.files/image182.gif)
※12..files/image184.gif)
.files/image186.gif)
※13..files/image057.gif)
.files/image189.gif)
.files/image191.gif)
※14..files/image193.gif) 记
记.files/image195.gif)
.files/image197.gif)
.files/image199.gif)
.files/image201.gif)
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
15(本题 13 分)
解:设.files/image203.gif) ,由
,由.files/image123.gif) 得
得.files/image205.gif) ;
;
.files/image207.gif) 是纯虚数,则
是纯虚数,则.files/image209.gif)
.files/image211.gif) ,
,.files/image213.gif)
16.(本题 13 分)
1)
.files/image214.jpg)
(2)
.files/image215.jpg)
(3)
.files/image216.jpg)
(4)
.files/image217.jpg)
17(本题 13 分)
解:设.files/image203.gif) ,而
,而.files/image138.gif) 即
即.files/image219.gif)
则.files/image221.gif)
18.(本题 13 分)
略
19.(本题 14 分)
解:首先求出函数.files/image144.gif) 的零点:
的零点:.files/image223.gif) ,
,.files/image225.gif) ,
,.files/image227.gif) .又易判断出在
.又易判断出在.files/image229.gif) 内,图形在
内,图形在.files/image146.gif) 轴下方,在
轴下方,在.files/image232.gif) 内,图形在
内,图形在.files/image146.gif) 轴上方,
轴上方,
所以所求面积为.files/image234.gif)
.files/image236.gif)
.files/image238.gif)
20.(本题 14 分)
解:(1)设f(x)=ax2+bx+c,则f′(x)=2ax+b,
又已知f′(x)=2x+2
∴a=1,b=2.
∴f(x)=x2+2x+c
又方程f(x)=0有两个相等实根,
∴判别式Δ=4-4c=0,即c=1.
故f(x)=x2+2x+1.
(2)依题意,有所求面积=.files/image240.gif) .
.
(3)依题意,有.files/image242.gif) ,
,
∴.files/image244.gif) ,-
,-.files/image246.gif) t3+t2-t+
t3+t2-t+.files/image246.gif) =
=.files/image246.gif) t3-t2+t,2t3-6t2+6t-1=0,
t3-t2+t,2t3-6t2+6t-1=0,
∴2(t-1)3=-1,于是t=1-.files/image248.gif) .
.
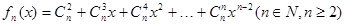 ,当
,当 且
且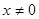 时,证明:
时,证明: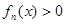 恒成立
恒成立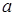 为实数,函数
为实数,函数 .
.  ,求
,求 的最小值;
的最小值;  ,直接写出(不需给出演算步骤)不等式
,直接写出(不需给出演算步骤)不等式 的解集.
的解集.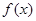 ,对任意
,对任意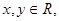 有
有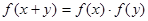 , 且当
, 且当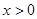 时,恒有
时,恒有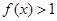 ,若
,若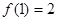 .
.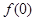 ;
;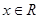 时
时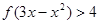 .
.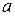 为实数,函数
为实数,函数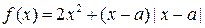 .
. ,求
,求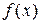 的最小值;
的最小值;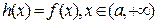 ,直接写出(不需给出演算步骤)不等式
,直接写出(不需给出演算步骤)不等式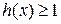 的解集.
的解集.