摘要:证明:(1)△A′B′C∽△ABC, (2)问点A′在弧DAC上什么位置时.S△A′B′C的面积最大.请说明理由, (3)当O1O2=11.CD=9时.求S△A′B′C的最大值.
网址:http://m.1010jiajiao.com/timu_id_692017[举报]
 22、阅读与理解:
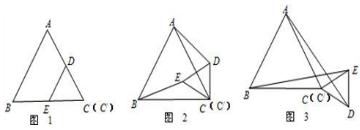
22、阅读与理解:图1是边长分别为a和b(a>b)的两个等边三角形纸片ABC和C′DE叠放在一起(C与C′重合)的图形.
操作与证明:
(1)操作:固定△ABC,将△C′DE绕点C按顺时针方向旋转30°,连接AD,BE,如图2;在图2中,线段BE与AD之间具有怎样的大小关系?证明你的结论;
(2)操作:若将图1中的△C′DE,绕点C按顺时针方向任意旋转一个角度α,连接AD,BE,如图3;在图3中,线段BE与AD之间具有怎样的大小关系?证明你的结论;
猜想与发现:
根据上面的操作过程,请你猜想当α为多少度时,线段AD的长度最大是多少?当α为多少度时,线段AD的长度最小是多少?
 证明命题“全等三角形对应边上的中线相等”是真命题.请填空并证明.
证明命题“全等三角形对应边上的中线相等”是真命题.请填空并证明.已知:如图,
△ABC≌△A′B′C′
△ABC≌△A′B′C′
,AD和A′D′分别是边BC,B′C′上的中线.求证:
AD=A′D′
AD=A′D′
.证明:
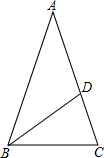 如图,△ABC中,点D在边AC上,且∠A=36°,∠DBC=36°,∠C=72°,
如图,△ABC中,点D在边AC上,且∠A=36°,∠DBC=36°,∠C=72°,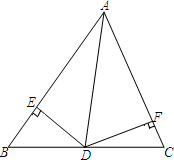 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,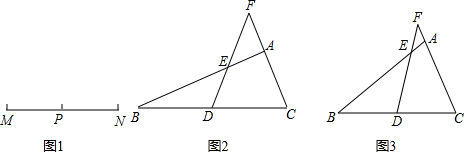 变,若BE=CF的结论仍然成立,请写出△AEF必须满足的条件,并加以证明.
变,若BE=CF的结论仍然成立,请写出△AEF必须满足的条件,并加以证明.