摘要:22.P是等边三角形ABC内的一点.连接PA.PB.PC.以BP为边作∠PBQ=60°.且BQ=BP.连接CQ.观察并猜想AP与CQ之间的大小关系.并证明你的结论.
网址:http://m.1010jiajiao.com/timu_id_691715[举报]
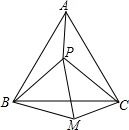 如图,P是等边三角形ABC内的一点,连接PA、PB、PC,以BP为边作等边三角形BPM,连接CM.
如图,P是等边三角形ABC内的一点,连接PA、PB、PC,以BP为边作等边三角形BPM,连接CM.(1)观察并猜想AP与CM之间的大小关系,并说明你的结论;
(2)若PA=PB=PC,则△PMC是
(3)若PA:PB:PC=1:
| 2 |
| 3 |
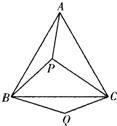 26、如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
26、如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.(1)观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2)若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由.
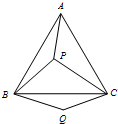 18、如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.观察并猜想AP与CQ之间的大小关系,并证明你的结论.试说明△ABP经过怎样变换可得到△CBQ.
18、如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.观察并猜想AP与CQ之间的大小关系,并证明你的结论.试说明△ABP经过怎样变换可得到△CBQ.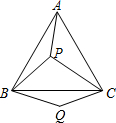 如图,P是等边三角形ABC内的一点,连接PA、PB、PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
如图,P是等边三角形ABC内的一点,连接PA、PB、PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ. ,连接CQ.
,连接CQ.