摘要:10+0.5210+l3
网址:http://m.1010jiajiao.com/timu_id_690581[举报]
观察下列两组算式,回答问题:
第一组 第二组
①0+1=12 ①0=
×1×0
②1+3=22 ②1=
×2×1
③3+6=32 ③3=
×3×2
④6+10=42 ④6=
×4×3
⑤
⑥
…
(1)根据第一组①→④式之间和本身所反映出的规律,继续完成第⑤⑥式(直接填在横线上);
(2)学习第二组对第一组各式第一个数的分析,寻找规律,将第一组的第n个式子表示出来.
查看习题详情和答案>>
第一组 第二组
①0+1=12 ①0=
| 1 |
| 2 |
②1+3=22 ②1=
| 1 |
| 2 |
③3+6=32 ③3=
| 1 |
| 2 |
④6+10=42 ④6=
| 1 |
| 2 |
⑤
10+15=52
10+15=52
⑥
15+21=62
15+21=62
…
(1)根据第一组①→④式之间和本身所反映出的规律,继续完成第⑤⑥式(直接填在横线上);
(2)学习第二组对第一组各式第一个数的分析,寻找规律,将第一组的第n个式子表示出来.
古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.观察下面的点阵图和相应的等式,探究其中的规律:
(1)下图反映了任何一个三角形数是如何得到的,认真观察,并在④后面的横线上写出相应的等式;

①1=1
②1+2=
=3
③1+2+3=
=6
④
(2)通过猜想,写出(1)中与第九个点阵相对应的等式
(3)从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.结合(1)观察下列点阵图,并在⑤看面的黄线上写出相应的等式.

①1=12
②1+3=22
③3+6=32
④6+10=42
⑤
(4)通过猜想,写出(3)中与第n个点阵相对应的等式
+
=n2
+
=n2;
(5)判断225是不是正方形数,如果不是,说明理由;如果是,225可以看作哪两个相邻的“三角形数”之和?
查看习题详情和答案>>
(1)下图反映了任何一个三角形数是如何得到的,认真观察,并在④后面的横线上写出相应的等式;

①1=1
②1+2=
| (1+2)×2 |
| 2 |
③1+2+3=
| (1+3)×3 |
| 2 |
④
1+2+3+4=
| (1+4)×4 |
| 2 |
1+2+3+4=
;| (1+4)×4 |
| 2 |
(2)通过猜想,写出(1)中与第九个点阵相对应的等式
1+2+3+…+9=
| (1+9)×9 |
| 2 |
1+2+3+…+9=
;| (1+9)×9 |
| 2 |
(3)从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.结合(1)观察下列点阵图,并在⑤看面的黄线上写出相应的等式.

①1=12
②1+3=22
③3+6=32
④6+10=42
⑤
10+15=52
10+15=52
;(4)通过猜想,写出(3)中与第n个点阵相对应的等式
| (1+n-1)(n-1) |
| 2 |
| (1+n)×n |
| 2 |
| (1+n-1)(n-1) |
| 2 |
| (1+n)×n |
| 2 |
(5)判断225是不是正方形数,如果不是,说明理由;如果是,225可以看作哪两个相邻的“三角形数”之和?
观察下面的点阵图和相应的等式,探究其中的规律:
(1)认真观察,并在④后面的横线上写出相应的等式.

①1=1 ②1+2=
=3 ③1+2+3=
=6 ④
(2)结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.

1=12 ②1+3=22 ③3+6=32 ④6+10=42 ⑤
(3)通过猜想,写出(2)中与第n个点阵相对应的等式
+
=n2
+
=n2.
查看习题详情和答案>>
(1)认真观察,并在④后面的横线上写出相应的等式.

①1=1 ②1+2=
| (1+2)×2 |
| 2 |
| (1+3)×3 |
| 2 |
1+2+3+4=
=10
| (1+4)×4 |
| 2 |
1+2+3+4=
=10
…| (1+4)×4 |
| 2 |
(2)结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.

1=12 ②1+3=22 ③3+6=32 ④6+10=42 ⑤
10+15=52
10+15=52
…(3)通过猜想,写出(2)中与第n个点阵相对应的等式
| n(n-1) |
| 2 |
| n(n+1) |
| 2 |
| n(n-1) |
| 2 |
| n(n+1) |
| 2 |
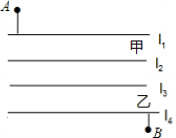 如图,五羊大学建立分校,校本部与分校隔着两条平行的小河,l1∥l2表示小河甲,l3∥l4表示小河乙,A为校本部大门,B为分校大门,为方便人员来往,要在两条小河上各建一座桥,桥面垂直于河岸.图中的尺寸是:甲河宽8米,乙河宽10米,A到甲河垂直距离为40米,B到乙河垂直距离为20米,两河距离100米,A、B两点水平距离(与小河平行方向)120米,为使A、B两点间来往路程最短,两座桥都按这个目标而建,那么,此时A、D两点间来往的路程是多少米?
如图,五羊大学建立分校,校本部与分校隔着两条平行的小河,l1∥l2表示小河甲,l3∥l4表示小河乙,A为校本部大门,B为分校大门,为方便人员来往,要在两条小河上各建一座桥,桥面垂直于河岸.图中的尺寸是:甲河宽8米,乙河宽10米,A到甲河垂直距离为40米,B到乙河垂直距离为20米,两河距离100米,A、B两点水平距离(与小河平行方向)120米,为使A、B两点间来往路程最短,两座桥都按这个目标而建,那么,此时A、D两点间来往的路程是多少米?