摘要:22.若.求代数式的值
网址:http://m.1010jiajiao.com/timu_id_686909[举报]
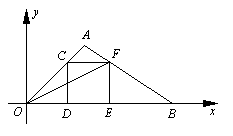
(本题满分12分)在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF. 连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.

1.⑴ 求tan∠FOB的值;
2.⑵用含t的代数式表示△OAB的面积S;
3.⑶是否存在点C,使以B,E,F为顶点的三角形与△OFE相似,若存在,请求出所有满足要求的B点的坐标;若不存在,请说明理由.
查看习题详情和答案>>
(本题6分)已知方程组 有两组实数解
有两组实数解 ,
, ,且
,且![]() ,
,![]() ,设
,设![]() ,
,
(1)求![]() 的取值范围;
的取值范围;
(2)用含![]() 的代数式表示
的代数式表示![]() ;(3)是否存在这样的
;(3)是否存在这样的![]() 的值,使
的值,使![]() 的值为—2 ?如果存在,求出这样的
的值为—2 ?如果存在,求出这样的 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看习题详情和答案>>
(本题满分13分)如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG.设E点移动距离为x(x>0).

⑴△EFG的边长是____(用含有x的代数式表示),当x=2时,点G的位置在_______;
⑵若△EFG与梯形ABCD重叠部分面积是y,求
①当0<x≤2时,y与x之间的函数关系式;
②当2<x≤6时,y与x之间的函数关系式;
⑶探求⑵中得到的函数y在x取含何值时,存在最大值,并求出最大值.
查看习题详情和答案>>
 值;
值; 的一元二次方程
的一元二次方程
 的两个实数根分别为
的两个实数根分别为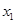 、
、 ,则
,则 ,
, 
 有两个非零不等实数根
有两个非零不等实数根 .
.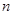 的取值范围;
的取值范围; ;
; 值,使
值,使