摘要：9．关于任意的实数.代数式的值是 A．正数 B．非负数 C． 整数 D．不能确定的数
网址：http://m.1010jiajiao.com/timu_id_686758[举报]
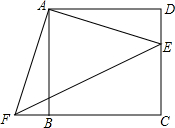如图所示，E是边长为12的正方形ABCD中CD上任意一点，以点A为中心，将△ADE顺时针旋转90°至△ABF的位置，设DE=t（1）用含t的代数式表示：△ABF的面积为S1，△CEF的面积为S2和△AEF的面积为S；
（2）求证：①S3＞S2 ，②S3≥2S1；
（3）若CE、DE的长度是关于x的一元二次方程x2-mx+3m-1-=0的两个实数根，求AF的值．
已知关于x的方程x2-2（k+1）x+k2+2k-
=0 ①．
（1）求证：对于任意实数k，方程①总有两个不相等的实数根；
（2）如果a是关于y的方程y2-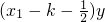
+（x1-k）（x2-k）+
=0 ②的根，其中x1、x2为方程①的两个实数根，且x1＜x2，求代数式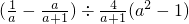
的值．
查看习题详情和答案>>
已知关于x的方程x2-2（k+1）x+k2+2k-
=0 ①．
（1）求证：对于任意实数k，方程①总有两个不相等的实数根；
（2）如果a是关于y的方程y2-(x1-k-
)y+（x1-k）（x2-k）+
=0 ②的根，其中x1、x2为方程①的两个实数根，且x1＜x2，求代数式(
-
)÷
•(a2-1)的值．
查看习题详情和答案>>
| 5 |
| 4 |
（1）求证：对于任意实数k，方程①总有两个不相等的实数根；
（2）如果a是关于y的方程y2-(x1-k-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| a |
| a |
| a+1 |
| 4 |
| a+1 |
已知关于x的方程x2-2（k+1）x+k2+2k-
=0 ①．
（1）求证：对于任意实数k，方程①总有两个不相等的实数根；
（2）如果a是关于y的方程y2-(x1-k-
)y+（x1-k）（x2-k）+
=0 ②的根，其中x1、x2为方程①的两个实数根，且x1＜x2，求代数式(
-
)÷
•(a2-1)的值．
查看习题详情和答案>>
| 5 |
| 4 |
（1）求证：对于任意实数k，方程①总有两个不相等的实数根；
（2）如果a是关于y的方程y2-(x1-k-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| a |
| a |
| a+1 |
| 4 |
| a+1 |
九年义务教育三年制初级中学教科书代数第三册中，有以下几段文字：“对于坐标平面内任意一点M，都有唯一的一对有序实数（x，y）和它对应；对于任意一对有序实数（x，y），在坐标平面内都有唯一的一点M和它对应，也就是说，坐标平面内的点与有序实数对是一一对应的．”“一般地，对于一个函数，如果把自变量x与函数y的每对对应值分别作为点的横坐标与纵坐标，在坐标平面内描出相应的点，这些点所组成的图形，就是这个函数的图象．”“实际上，所有一次函数的图象都是一条直线．”“因为两点确定一条直线，所以画一次函数的图象时，只要先描出两点，再连成直线，就可以了．”由此可知：满足函数关系式的有序实数对所对应的点，一定在这个函数的图象上；反之，函数图象上的点的坐标，一定满足这个函数的关系式．另外，已知直线上两点的坐标，便可求出这条直线所对应的一次函数的解析式．问题1：已知点A（m，1）在直线y=2x-1上，求m的方法是：
问题2：已知某个一次函数的图象经过点P（3，5）和Q（-4，-9），求这个一次函数的解析式时，一般先