网址：http://m.1010jiajiao.com/timu_id_68607[举报]
（09年湖北补习学校联考文）（14分）已知椭圆的一个焦点
，对应的准线方程为
，且离心率
满足
，，
成等比数列.
(1)求椭圆的方程；
(2)试问是否存在直线
，使与椭圆交于不同的两点
、
，且线段
恰被直线
平分？若存在，求出的倾斜角的取值范围；若不存在，请说明理由.
|
（本题满分16分）第（1）小题满分4分，第（2）小题满分6分，第（3）小题满分6分。 定义：由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”。如果两个椭圆的“特征三角形”是相似的，则称这两个椭圆是“相似椭圆”，并将三角形的相似比称为椭圆的相似比。已知椭圆。 若椭圆，判断与是否相似？如果相似，求出与的相似比；如果不相似，请说明理由；
如图：直线与两个“相似椭圆”和分别交于点和点， 试在椭圆和椭圆上分别作出点和点（非椭圆顶点），使和组成以为相似比的两个相似三角形，写出具体作法。（不必证明） 查看习题详情和答案>> 上海市徐汇区2011届高三下学期学习能力诊断卷（数学理）.doc | | |
|
写出与椭圆相似且短半轴长为的椭圆的方程；若在椭圆上存在两点、关于直线对称，求实数的取值范围？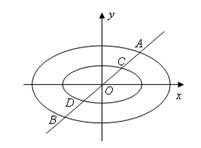
写出与椭圆相似且短半轴长为的椭圆的方程；若在椭圆上存在两点、关于直线对称，求实数的取值范围？