摘要：如果图1中的圆圈共有12层.(1)我们自上往下.在每个圆圈中都按图3的方式填上一串连续的正整数.则最底层最左边这个圆圈中的数是 ,(2)我们自上往下.在每个圆圈中都按图4的方式填上一串连续的整数....求图4中所有圆圈中各数的绝对值之和．
网址：http://m.1010jiajiao.com/timu_id_685412[举报]
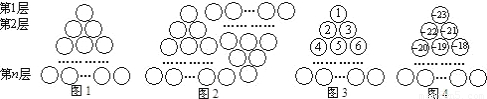
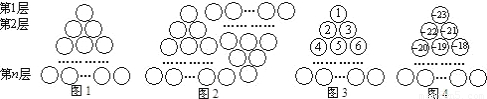
图1是由若干个小圆圈堆成的一个形如正三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共堆了
层．将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为
．
如果图1中的圆圈共有12层，（1）我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数
，则最底层最左边这个圆圈中的数是 ；（2）我们自上往下，在每个圆圈中都按图4的方式填上一串连续的整数
，
，
，
，求图4中所有圆圈中各数的绝对值之和．
图1是由若干个小圆圈堆成的一个形如正三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共堆了n层，将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为
。
。
如果图1中的圆圈共有12层，（1）我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数，则最底层最左边这个圆圈中的数是____；
（2）我们自上往下，在每个圆圈中都按图4的方式填上一串连续的整数，-23，-22，-21，求图4中所有圆圈中各数的绝对值之和。
查看习题详情和答案>>
（2）我们自上往下，在每个圆圈中都按图4的方式填上一串连续的整数，-23，-22，-21，求图4中所有圆圈中各数的绝对值之和。
图1是由若干个小圆圈堆成的一个形如正三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共堆了n层．将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为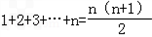
．
(无法处理)
如果图1中的圆圈共有12层，我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数1，2，3，4，…，则最底层最左边这个圆圈中的数是（ ）．
查看习题详情和答案>>
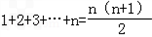．(无法处理)如果图1中的圆圈共有12层，我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数1，2，3，4，…，则最底层最左边这个圆圈中的数是（ ）．
．
．
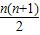
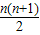