摘要:(1)分别求出和时与的函数表达式,(2)小明家第二季度交纳水费的情况如下:月份四月份五月份六月份交费金额30元34元
网址:http://m.1010jiajiao.com/timu_id_685347[举报]
如图,l 1,l 2分别表示一种白炽灯和一种节能灯的费用y元(费用灯的售价+电费)与照明时间x小时的函数图象,假设两种灯的使用寿命都是2000小时,照明效果一样。

(1)根据图象求l 1,l 2的函数表达式;
(2)当照明时间为多少时,两种费用相等?
(3)小亮房间计划照明2500小时,他买了一个白炽灯和一个节能灯,请你帮助设计一种最省钱的方案(直接给出答安,不必写过程)
查看习题详情和答案>>
(2)当照明时间为多少时,两种费用相等?
(3)小亮房间计划照明2500小时,他买了一个白炽灯和一个节能灯,请你帮助设计一种最省钱的方案(直接给出答安,不必写过程)
某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20![]() 时,按2元/
时,按2元/![]() 计费;月用水量超过20
计费;月用水量超过20![]() 时,其中的20
时,其中的20![]() 仍按2元/
仍按2元/![]() 收费,超过部分按
收费,超过部分按![]() 元/
元/![]() 计费.设每户家庭用用水量为
计费.设每户家庭用用水量为![]() 时,应交水费
时,应交水费![]() 元.
元.
(1)
分别求出(2)
小明家第二季度交纳水费的情况如下:![]()
小明家这个季度共用水多少立方米?
查看习题详情和答案>>
某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20![]() 时,按2元/
时,按2元/![]() 计费;月用水量超过20
计费;月用水量超过20![]() 时,其中的20
时,其中的20![]() 仍按2元/
仍按2元/![]() 收费,超过部分按
收费,超过部分按![]() 元/
元/![]() 计费.设每户家庭用用水量为
计费.设每户家庭用用水量为![]() 时,应交水费
时,应交水费![]() 元.
元.
(1
)分别求出(2
)小明家第二季度交纳水费的情况如下:|
月份 |
四月份 |
五月份 |
六月份 |
|
交费金额 |
30 元 |
34 元 |
42.6 元 |
小明家这个季度共用水多少立方米?
查看习题详情和答案>>
如图1,在平面直角坐标系中,拋物线y=ax2+c与x轴正半轴交于点F(16,0)、与y轴正半轴交于点E(0,16),边长为16的正方形ABCD的顶点D与原点O重合,顶点A与点E重合,顶点C与点F重合;
【小题1】求拋物线的函数表达式
【小题2】如图2,若正方形ABCD在平面内运动,并且边BC所在的直线始终与x轴垂直,抛物线始终与边AB交于点P且同时与边CD交于点Q(运动时,点P不与A、B两点重合,点Q不与C、D两点重合)。设点A的坐标为(m,n) (m>0)。
j当PO=PF时,分别求出点P和点Q的坐标;
k在j的基础上,当正方形ABCD左右平移时,请直接写出m的取值范围;
l当n=7时,是否存在m的值使点P为AB边中点。若存在,请求出m的值;若不存在,请说明理由。 查看习题详情和答案>>
查看习题详情和答案>>
【小题1】求拋物线的函数表达式
【小题2】如图2,若正方形ABCD在平面内运动,并且边BC所在的直线始终与x轴垂直,抛物线始终与边AB交于点P且同时与边CD交于点Q(运动时,点P不与A、B两点重合,点Q不与C、D两点重合)。设点A的坐标为(m,n) (m>0)。
j当PO=PF时,分别求出点P和点Q的坐标;
k在j的基础上,当正方形ABCD左右平移时,请直接写出m的取值范围;
l当n=7时,是否存在m的值使点P为AB边中点。若存在,请求出m的值;若不存在,请说明理由。
 查看习题详情和答案>>
查看习题详情和答案>>
某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20 时,按2元/
时,按2元/ 计费;月用水量超过20
计费;月用水量超过20 时,其中的20
时,其中的20 仍按2元/
仍按2元/ 收费,超过部分按
收费,超过部分按 元/
元/ 计费.设每户家庭用用水量为
计费.设每户家庭用用水量为 时,应交水费
时,应交水费 元.
元.
(1)分别求出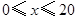 和
和 时
时 与
与 的函数表达式;
的函数表达式;
(2)小明家第二季度交纳水费的情况如下:
| 月份 | 四月份 | 五月份 | 六月份 |
| 交费金额 | 30元 | 34元 | 42.6元 |