摘要:20.聪明的小明发现:...-则(.都是正整数)时.的值应是 .
网址:http://m.1010jiajiao.com/timu_id_683073[举报]
今年“十一”黄金假期(1日到7日)期间,鼓楼购物中心决定连续若干天举行促销活动.原来销售一种西装和领带,西装每套定价500元,领带每条定价80元.开展促销活动期间,向客户提供两种优惠方案:
①买一套西装送一条领带;
②西装和领带都按定价的90%付款.
现某客户要到鼓楼购物中心购买西装20套,领带x条 (x>20)
(1)若该客户按方案①购买,需付款
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)聪明的小明发现促销的日期数之和恰好为15,请你直接写出此次促销的起止日期.
查看习题详情和答案>>
①买一套西装送一条领带;
②西装和领带都按定价的90%付款.
现某客户要到鼓楼购物中心购买西装20套,领带x条 (x>20)
(1)若该客户按方案①购买,需付款
(8400+80x)
(8400+80x)
元(用含x的代数式表示);若该客户按方案②购买,需付款(9000+72x)
(9000+72x)
元(用含x的代数式表示);(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)聪明的小明发现促销的日期数之和恰好为15,请你直接写出此次促销的起止日期.
今年“十一”黄金假期(1日到7日)期间,鼓楼购物中心决定连续若干天举行促销活动.原来销售一种西装和领带,西装每套定价500元,领带每条定价80元.开展促销活动期间,向客户提供两种优惠方案:
①买一套西装送一条领带;
②西装和领带都按定价的90%付款.
现某客户要到鼓楼购物中心购买西装20套,领带x条 (x>20)
(1)若该客户按方案①购买,需付款______元(用含x的代数式表示);若该客户按方案②购买,需付款______元(用含x的代数式表示);
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)聪明的小明发现促销的日期数之和恰好为15,请你直接写出此次促销的起止日期.
查看习题详情和答案>>
提出问题:小明是个爱思考的学生,在学习了三角函数后小明发现:
sin90°=1,sin45°=
,90°是45°的两倍,但三角函数值却是
倍;
sin30°= ,sin60°= ,60°是30°的两倍,但三角函数值却是 倍,
考虑到cos45°,cos30°的三角函数值,估计sin2α=2sinαcosα,代入检验发现以上两组角度都符合.
解决问题:那么如何证明sin2α=2sinαcosα呢?
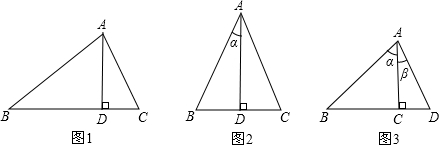
小明思考再三,发现在△ABC中(图2),高AD=ABsinB,可得S△ABC=
BC•ABsinB,
利用这个结论证明上述命题结论.聪明的你也能解决这个问题吗?
如图2,在△ABC中,AB=AC,AD⊥BC于D,设∠BAD=α,求证:sin2α=2sinαcosα.
推广应用:解决了以上问题后,小明思考再三,终于发现了sin(α+β)与sinα,cosα,sinβ,cosβ的关系,
你能结合图3证明出自己所猜想的sin(α+β)与sinα,cosα,sinβ,cosβ的关系吗?
并利用上述关系求出sin75°的值(保留根号).
 查看习题详情和答案>>
查看习题详情和答案>>
sin90°=1,sin45°=
| ||
| 2 |
| 2 |
sin30°=
考虑到cos45°,cos30°的三角函数值,估计sin2α=2sinαcosα,代入检验发现以上两组角度都符合.
解决问题:那么如何证明sin2α=2sinαcosα呢?
小明思考再三,发现在△ABC中(图2),高AD=ABsinB,可得S△ABC=
| 1 |
| 2 |
利用这个结论证明上述命题结论.聪明的你也能解决这个问题吗?
如图2,在△ABC中,AB=AC,AD⊥BC于D,设∠BAD=α,求证:sin2α=2sinαcosα.
推广应用:解决了以上问题后,小明思考再三,终于发现了sin(α+β)与sinα,cosα,sinβ,cosβ的关系,
你能结合图3证明出自己所猜想的sin(α+β)与sinα,cosα,sinβ,cosβ的关系吗?
并利用上述关系求出sin75°的值(保留根号).
 查看习题详情和答案>>
查看习题详情和答案>>
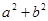 、
、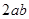 、
、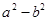 (a、b都是正整数),则这个三角形是()
(a、b都是正整数),则这个三角形是()