网址:http://m.1010jiajiao.com/timu_id_680784[举报]
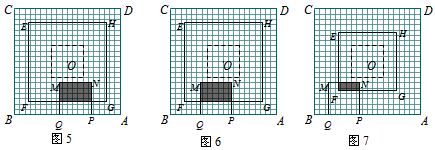
(1)请你在图2和图3中分别画出x为2秒、18秒时,正方形EFGH和正方形MNPQ的位置及重叠部分(重叠部分用阴影表示),并分别写出重叠部分的面积;
(2)①如图4,当1≤x≤3.5时,求y与x的函数关系式;
②如图5,当3.5≤x≤7时,求y与x的函数关系式;
③如图6,当7≤x≤10.5时,求y与x的函数关系式;
④如图7,当10.5≤x≤13时,求y与x的函数关系式;
(3)对于正方形MNPQ在正方形ABCD各边上移动一周的过程,请你根据重叠部分面积y的变化情况,指出y取得最大值和最小值时,相对应的x的取值情况,并指出最大值和最小值分别是多少。

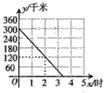
(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,两车相距的路程为s(千米),请直接写出s关于x的表达式,不需要求x的取值范围;
(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为a(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度a,画出乙车离开B 城高速公路人口处的距离y(千米)与行驶时间x(时)之间的函数图象。
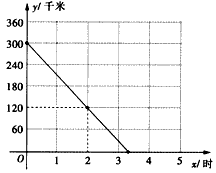
(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,两车相距的路程为s(千米),请直接写出s关于x的表达式;
(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为a(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度a,在下图中画出乙车离开B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的函数图象。
某单位团支部组织青年团员参加登山比赛。比赛奖次所设等级分为:一等奖1人,二等奖4人,三等奖5人。团支部要求一等奖奖品单价比二等奖奖品单价高15元,二等奖奖品单价比三等奖奖品单价高15元。设一等奖奖品的单价为x(元),团支部购买奖品总金额为y(元)。
(1)求y与x的函数关系式(即函数表达式);
(2)因为团支部活动经费有限,购买奖品的总金额应限制在:![]() 。在这种情况下,请根据备选奖品表提出购买一、二、三等奖奖品有哪几种方案?然后本着尽可能节约资金的原则,选出最佳方案,并求出这时全部奖品所需总金额是多少?
。在这种情况下,请根据备选奖品表提出购买一、二、三等奖奖品有哪几种方案?然后本着尽可能节约资金的原则,选出最佳方案,并求出这时全部奖品所需总金额是多少?
备选奖品及单价如下表(单价:元)
备选奖品 | 足球 | 篮球 | 排球 | 羽毛球拍 | 乒乓球拍 | 旱冰鞋 | 运动衫 | 象棋 | 围棋 |
单价(元) | 84 | 79 | 74 | 69 | 64 | 59 | 54 | 49 | 44 |
查看习题详情和答案>>
在“春季经贸洽谈会”上,我市某服装厂接到生产一批出口服装的订单,要求必须在12天(含12天)内保质保量完成,且当天加工的服装当天立即空运走。为了加快进度,车间采取工人轮流休息,机器满负荷运转的生产方式,生产效率得到了提高。这样每天生产的服装数量y(套)与时间x(元)的关系如下表

由于机器损耗等原因,当每天生产的服装数达到一定量后,平均每套服装的成本会随着服装产量的增加而增大,这样平均每套服装的成本z(元)与生产时间x(天)的关系如图所示.

1.判断每天生产的服装的数量y(套)与生产时间x(元)之间是我们学过的哪种函数关系?并验证
2.已知这批外贸服装的订购价格为每套1570元,设车间每天的利润为w(元).求w(元)与x(天)之间的函数关系式,并求出哪一天该生产车间获得最高利润,最高利润是多少元?
3.从第6天起,该厂决定该车间每销售一套服装就捐a元给山区的留守儿童作为建图书室的基金,但必须保证每天扣除捐款后的利润随时间的增大而增大.求a的最大值,此时留守儿童共得多少元基金
查看习题详情和答案>>