摘要：13．请写出一个以2为其中一根的一元二次方程 ,
网址：http://m.1010jiajiao.com/timu_id_680041[举报]
（1）先化简，再求值：(x+2-
)÷
，其中x=
-3；
（2）若a=1-
，先化简再求
+
的值；
（3）已知a=
+1，b=
-1，求a2-a2005b2006+b2的值；
（4）已知：实数a，b在数轴上的位置如图所示，
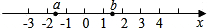
化简：
+2
-|a-b|；
（5）观察下列各式及验证过程：
N=2时有式①：2×
=
N=3时有式②：3×
=
式①验证：2×
=
=
=
=
式②验证：3×
=
=
=
=
①针对上述式①、式②的规律，请写出n=4时变化的式子；
②请写出满足上述规律的用n（n为任意自然数，且n≥2）表示的等式，并加以验证．
（6）已知关于x的一元二次方程x2+（2m-1）+m2=0有两个实数根x1和x2． ①求实数m的取值范围；②当x12-x22=0时，求m的值． 查看习题详情和答案>>
| 5 |
| x-2 |
| x-3 |
| x-2 |
| 5 |
（2）若a=1-
| 2 |
| a2-1 |
| a2+a |
| ||
| a2-a |
（3）已知a=
| 2 |
| 2 |
（4）已知：实数a，b在数轴上的位置如图所示，
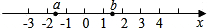
化简：
| (a+1)2 |
| (b-1)2 |
（5）观察下列各式及验证过程：
N=2时有式①：2×
|
2+
|
N=3时有式②：3×
|
3+
|
式①验证：2×
|
|
|
|
2+
|
式②验证：3×
|
|
|
|
3+
|
①针对上述式①、式②的规律，请写出n=4时变化的式子；
②请写出满足上述规律的用n（n为任意自然数，且n≥2）表示的等式，并加以验证．
（6）已知关于x的一元二次方程x2+（2m-1）+m2=0有两个实数根x1和x2． ①求实数m的取值范围；②当x12-x22=0时，求m的值． 查看习题详情和答案>>
如图，
ABCD在平面直角坐标系中，AD=6，若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根，且OA＞OB。
（1）写出A、B两点的坐标；
（2）若E为x正半轴上的点，且S△AOE=
，求经过D、E 两点的直线的解析式，并判断△AOE与△DAO是否相似？
（3）若点M在平面直角坐标系内，则在直线AB上是否存在点F使以A、C、F、M为顶点的四边形为菱形？若存在，请直接写出其中两个F点的坐标；若不存在，请说明理由。
ABCD在平面直角坐标系中，AD=6，若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根，且OA＞OB。（1）写出A、B两点的坐标；
（2）若E为x正半轴上的点，且S△AOE=
，求经过D、E 两点的直线的解析式，并判断△AOE与△DAO是否相似？（3）若点M在平面直角坐标系内，则在直线AB上是否存在点F使以A、C、F、M为顶点的四边形为菱形？若存在，请直接写出其中两个F点的坐标；若不存在，请说明理由。
小颖家离学校1200米，其中有一段为上坡路，另一段为下坡路．她去学校共用了16分钟．假设小颖上坡路的平均速度是3千米/时，下坡路的平均速度是5千米/时．请你根据以上信息，就小颖行走的“路程”或“时间”，先提出一个用二元一次方程组解决的问题，并写出解答过程．
查看习题详情和答案>>
中央综治委在对全国各省市自治区2010年社会治安综合治理考评中，重庆市以93.48分居全国第一，成为全国最安全、最稳定的城市之一． 市政府非常重视交巡警平台的建设，据统计，某行政区在去年前7个月内，交巡警平台的数量与月份之间的关系如下表：
| 月份x（月） | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 交巡警平台数量y1（个） | 32 | 34 | 36 | 38 | 40 | 42 | 44 |
（1）请观察表格，用所学过的一次函数、反比例函数或二次函数的有关知识，直接写出y1与x之间的函数关系式，根据如图所示的变化趋势，直接写出y2与x之间满足的一次函数关系式；
（2）2012年一月份，政府计划该区的交巡警平台数量比去年12份减少a%，在去年12月份的基础上每一个交巡警平台所需的资金量将增加0.1a%，某民营企业为表示对“平安重庆”的鼎力支持，决定在1月份对每个交巡警平台分别赞助30000元．若政府计划一月份用于交巡警平台的资金总额为126万元，请参考以下数据，估计a的整数值．
（参考数据：872=7569，882=7744，892=7921） 查看习题详情和答案>>