摘要:3.3比m小-6的数是 .当m=7时.这个数是 .
网址:http://m.1010jiajiao.com/timu_id_679918[举报]
29、你能比较两个数20092008和20082009的大小吗?
为了解决这个问题,我们首先把它抽象成一般形式,即比较(n+1)n和nn+1的大小(n为自然数),我们分析时从特殊向简单的情形入手,通过对n=1,n=2,n=3,…时的分析,从中发现规律,经过归纳,猜想出结论.
(1)计算,比较下列各组数中两个数大小(在空格中填“>”、“=”、“<”)12
(2)从上面的结果进行归纳猜想,nn+1和(n+1)n的大小关系是:.
①当n=1和n=2时,
②当
(3)根据上面的归纳猜想的规律,试比较20092008和20082009的大小.
查看习题详情和答案>>
为了解决这个问题,我们首先把它抽象成一般形式,即比较(n+1)n和nn+1的大小(n为自然数),我们分析时从特殊向简单的情形入手,通过对n=1,n=2,n=3,…时的分析,从中发现规律,经过归纳,猜想出结论.
(1)计算,比较下列各组数中两个数大小(在空格中填“>”、“=”、“<”)12
<
21,23<
32,34>
43,45>
54,56>
65,67>
76(2)从上面的结果进行归纳猜想,nn+1和(n+1)n的大小关系是:.
①当n=1和n=2时,
nn+1<(n+1)n
;②当
n≥3
时,nn+1>(n+1)n
.(3)根据上面的归纳猜想的规律,试比较20092008和20082009的大小.
35、你能比较两个数20062007和20072006的大小吗?为了解决这个问题,先把问题一般化,即比较nn+1和(n+1)n的大小(n≥1的整数).然后从分析n=1,n=2,n=3…这些简单情形入手,从中发现规律,经过归纳,猜想出结论.
(1)通过计算:比较①~⑦各组两个数的大小(在横线上填“>”“=”“<”)
①12
⑥67
(2)从上面各小题目的结果经过归纳,可以猜想出nn+1和(n+1)n的大小关系是nn+1
(3)根据上面归纳猜想到的结论,可以得到20062007
查看习题详情和答案>>
(1)通过计算:比较①~⑦各组两个数的大小(在横线上填“>”“=”“<”)
①12
<
21;②23<
32;③34>
43;④45>
54;⑤56>
65;⑥67
>
76;⑦78>
87;(2)从上面各小题目的结果经过归纳,可以猜想出nn+1和(n+1)n的大小关系是nn+1
当n=1或n=2时,n n+1<(n+1)n;当n≥3时,nn+1>(n+1)n;
(n+1)n(3)根据上面归纳猜想到的结论,可以得到20062007
>
20072006(填“>”“=”“<”)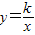 (k≠0)的图象经过点(-2,3),则这个函数的表达式是 .当x<0时,y的值随自变量x的增大而 (填“增大或减小”).
(k≠0)的图象经过点(-2,3),则这个函数的表达式是 .当x<0时,y的值随自变量x的增大而 (填“增大或减小”).