摘要:故平面 5分
网址:http://m.1010jiajiao.com/timu_id_67891[举报]
若近似地认为月球绕地球公转与地球绕日公转的轨道在同一平面内,且均为正圆,又知这两种转动同向,如下图所示,月相变化的周期为29.5天(图中是相继两次满月时月、地、日相对位置示意图).地球绕日旋转一周约需365.25天,求月球绕地球一周所用的时间T(因月球总是一面朝向地球,故T恰是月球的自转周期);其间月球绕地球转动了多少周?(精确到百分位)
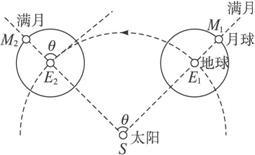
若近似地认为月球绕地球公转与地球绕日公转的轨道在同一个平面内,且均为正圆,又知这两种转动同向,如下图所示,月相变化的周期为29.5天(图中是相继两次满月时月、地、日相对位置示意图)
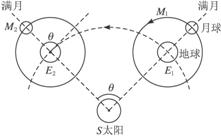
(1)求月球绕地球一周所用的时间T(因月球总是一面朝向地球,故T恰是月球自转周期);
(2)地球绕日旋转一周约需要365.25天,期间月球绕地球转动了多少圈?(精确百分位)
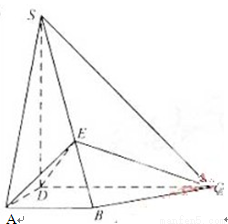
查看习题详情和答案>>如图,四棱锥S—ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的三等分点,SE=2EB
(Ⅰ)证明:平面EDC⊥平面SBC.(Ⅱ)求二面角A—DE—C的大小 .
【解析】本试题主要考查了立体几何中的运用。
(1)证明:因为SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的三等分点,SE=2EB 所以ED⊥BS,DE⊥EC,所以ED⊥平面SBC.,因此可知得到平面EDC⊥平面SBC.
(Ⅱ)由SA2= SD2+AD2 = 5 ,AB=1,SE=2EB,AB⊥SA,知
AE2= (1 /3 SA)2+(2/ 3 AB)2 =1,又AD=1.
故△ADE为等腰三角形.
取ED中点F,连接AF,则AF⊥DE,AF2= AD2-DF2 =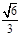 .
.
连接FG,则FG∥EC,FG⊥DE.
所以,∠AFG是二面角A-DE-C的平面角.
连接AG,AG= 2 ,FG2= DG2-DF2
=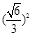 ,
,
cos∠AFG=(AF2+FG2-AG2 )/2⋅AF⋅FG =-1 /2 ,
所以,二面角A-DE-C的大小为120°
查看习题详情和答案>>