摘要:21.如图.表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图像(分别是正比例函数图像和一次函数图像).根据图像解答下列问题:(1)根据图象.轮船比快艇早出发 小时.(2)请分别求出表示轮船和快艇行驶过程的函数解析式(不要求写出自变量的取值范围),(3)通过计算说明快艇出发多长时间赶上轮船?
网址:http://m.1010jiajiao.com/timu_id_676351[举报]
(本题满分10分)如图,自来水厂A和村庄B在小河l的两侧,现要在A,B间铺设一知输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏东49°方向,B位于南偏西41°方向.
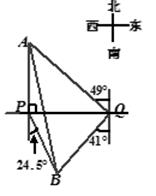
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A,B间的距离.(参考数据cos41°=0.75) 查看习题详情和答案>>

(1)线段BQ与PQ是否相等?请说明理由;
(2)求A,B间的距离.(参考数据cos41°=0.75) 查看习题详情和答案>>
(本题满分6分)如图,有一段斜坡BC长为10米,坡角∠CBD=12°,为方便残疾人的轮椅车通行,现准备把坡角降为5°.
【小题1】(1)求坡高CD;
【小题2】(2)求斜坡新起点A与原起点B的距离(精确到0.1米).
(本题满分6分)如图,有一段斜坡BC长为10米,坡角∠CBD=12°,为方便残疾人的轮椅车通行,现准备把坡角降为5°.
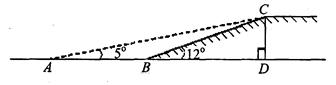
【小题1】(1)求坡高CD;
【小题2】(2)求斜坡新起点A与原起点B的距离(精确到0.1米). 查看习题详情和答案>>
查看习题详情和答案>>

【小题1】(1)求坡高CD;
【小题2】(2)求斜坡新起点A与原起点B的距离(精确到0.1米).
 查看习题详情和答案>>
查看习题详情和答案>>
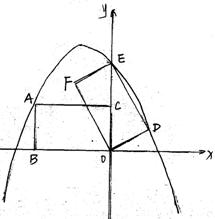
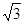 ,矩形ABOC绕点O按顺时针方向旋转60°后得矩形EFOD. 点A的对应点为点E,点B的对应点为F,点C的对应点为点D. 抛物线
,矩形ABOC绕点O按顺时针方向旋转60°后得矩形EFOD. 点A的对应点为点E,点B的对应点为F,点C的对应点为点D. 抛物线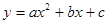 过点A、E、D.
过点A、E、D.