摘要:(2)当点在射线上运动(点与点不重合)时.与交于点.设.=.求关于的函数解析式.并写出函数的定义域,
网址:http://m.1010jiajiao.com/timu_id_675518[举报]
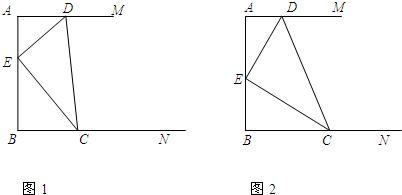
已知:![]() ,点
,点![]() 在射线
在射线![]() 上,
上,![]() (如图).
(如图).![]() 为直线
为直线![]() 上一动点,以
上一动点,以![]() 为边作等边三角形
为边作等边三角形![]() (点
(点![]() 按顺时针排列),
按顺时针排列),![]() 是
是![]() 的外心.
的外心.
(1)当点![]() 在射线
在射线![]() 上运动时,求证:点
上运动时,求证:点![]() 在
在![]() 的平分线上;
的平分线上;
(2)当点![]() 在射线
在射线![]() 上运动(点
上运动(点![]() 与点
与点![]() 不重合)时,
不重合)时,![]() 与
与![]() 交于点
交于点![]() ,设
,设![]() ,
,![]() =
=![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
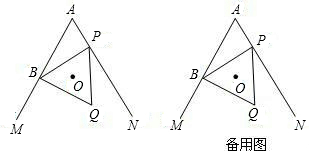
(3)若点![]() 在射线
在射线![]() 上,
上,![]() ,圆
,圆![]() 为
为![]() 的内切圆.当
的内切圆.当![]() 的边
的边![]() 或
或![]() 与圆
与圆![]() 相切时,请直接写出点
相切时,请直接写出点![]() 与点
与点![]() 的距离.
的距离.
 |
已知:![]() ,点
,点![]() 在射线
在射线![]() 上,
上,![]() (如图).
(如图).![]() 为直线
为直线![]() 上一动点,以
上一动点,以![]() 为边作等边三角形
为边作等边三角形![]() (点
(点![]() 按顺时针排列),
按顺时针排列),![]() 是
是![]() 的外心.
的外心.
(1
)当点(2
)当点(3
)若点
![]() 是等边三角形,点
是等边三角形,点![]() 是射线
是射线![]() 上的一个动点(点
上的一个动点(点![]() 不与点
不与点![]() 重合),
重合),![]() 是以
是以![]() 为边的等边三角形,过点
为边的等边三角形,过点![]() 作
作![]() 的平行线,分别交射线
的平行线,分别交射线![]() 于点
于点![]() ,连接
,连接![]() .
.
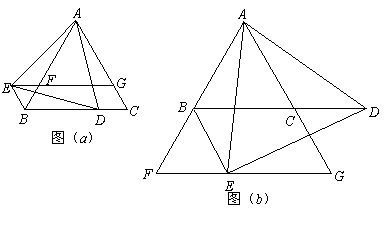
(1)如图(a)所示,当点![]() 在线段
在线段![]() 上时.
上时.
①求证:![]() ;
;
②探究四边形![]() 是怎样特殊的四边形?并说明理由;
是怎样特殊的四边形?并说明理由;
(2)如图(b)所示,当点![]() 在
在![]() 的延长线上时,直接写出(1)中的两个结论是否成立?
的延长线上时,直接写出(1)中的两个结论是否成立?
(3)在(2)的情况下,当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 是菱形?并说明理由.
是菱形?并说明理由.
 |
查看习题详情和答案>>