摘要:(1)当点在射线上运动时.求证:点在的平分线上,
网址:http://m.1010jiajiao.com/timu_id_675517[举报]
已知:![]() ,点
,点![]() 在射线
在射线![]() 上,
上,![]() (如图).
(如图).![]() 为直线
为直线![]() 上一动点,以
上一动点,以![]() 为边作等边三角形
为边作等边三角形![]() (点
(点![]() 按顺时针排列),
按顺时针排列),![]() 是
是![]() 的外心.
的外心.
(1)当点![]() 在射线
在射线![]() 上运动时,求证:点
上运动时,求证:点![]() 在
在![]() 的平分线上;
的平分线上;
(2)当点![]() 在射线
在射线![]() 上运动(点
上运动(点![]() 与点
与点![]() 不重合)时,
不重合)时,![]() 与
与![]() 交于点
交于点![]() ,设
,设![]() ,
,![]() =
=![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(3)若点![]() 在射线
在射线![]() 上,
上,![]() ,圆
,圆![]() 为
为![]() 的内切圆.当
的内切圆.当![]() 的边
的边![]() 或
或![]() 与圆
与圆![]() 相切时,请直接写出点
相切时,请直接写出点![]() 与点
与点![]() 的距离.
的距离.
 |
已知:![]() ,点
,点![]() 在射线
在射线![]() 上,
上,![]() (如图).
(如图).![]() 为直线
为直线![]() 上一动点,以
上一动点,以![]() 为边作等边三角形
为边作等边三角形![]() (点
(点![]() 按顺时针排列),
按顺时针排列),![]() 是
是![]() 的外心.
的外心.
(1
)当点(2
)当点(3
)若点
已知:∠MAN=60°,点B在射线AM上,AB=4(如图).P为直线AN上一动点,以BP为边作等边三角形BPQ(点B,P,Q按顺时针排列),O是△BPQ的外心.

(1)当点P在射线AN上运动时,求证:点O在∠MAN的平分线上;
(2)当点P在射线AN上运动(点P与点A不重合)时,AO与BP交于点C,设AP=x,AC·AO=y,求y关于x的函数解析式,并写出函数的定义域;
(3)若点D在射线AN上,AD=2,圆I为△ABD的内切圆.当△BPQ的边BP或BQ与圆I相切时,请直接写出点A与点O的距离.
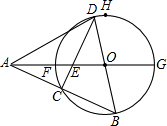 如图,点A在⊙O外,射线AO与⊙O交于F、G两点,点H在⊙O上,弧FH=弧GH,点D是弧FH上一个动点(不运动至F),BD是⊙O的直径,连接AB,交⊙O于点C,连接CD,交AO于点E,且OA=
如图,点A在⊙O外,射线AO与⊙O交于F、G两点,点H在⊙O上,弧FH=弧GH,点D是弧FH上一个动点(不运动至F),BD是⊙O的直径,连接AB,交⊙O于点C,连接CD,交AO于点E,且OA=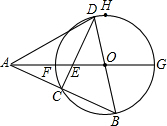 如图,点A在⊙O外,射线AO与⊙O交于F、G两点,点H在⊙O上,弧FH=弧GH,点D是弧FH上一个动点(不运动至F),BD是⊙O的直径,连接AB,交⊙O于点C,连接CD,交AO于点E,且OA=
如图,点A在⊙O外,射线AO与⊙O交于F、G两点,点H在⊙O上,弧FH=弧GH,点D是弧FH上一个动点(不运动至F),BD是⊙O的直径,连接AB,交⊙O于点C,连接CD,交AO于点E,且OA= ,OF=1,设AC=x,AB=y.
,OF=1,设AC=x,AB=y.