摘要:中的点M的坐标改为(5.0).其它条件不变.如图③.请直接写出符合条件的等腰三角形有几个.七.
网址:http://m.1010jiajiao.com/timu_id_675416[举报]
(1)如图,A1,A2,A3是抛物线y=
x2图象上的三点,若A1,A2,A3三点的横坐标从左至右依次为1,2,3.求△A1A2A3的面积.
(2)若将(1)问中的抛物线改为y=
x2-
x+2和y=ax2+bx+c(a>0),其他条件不变,请分别直接写出两种情况下△A1A2A3的面积.
(3)现有一抛物线组:y1=
x2-
x;y2=
x2-
x;y3=
x2-
x;y4=
x2-
x;y5=
x2-
x;…依据变化规律,请你写出抛物线组第n个式子yn的函数解析式;现在x轴上有三点A(1,0),B(2,0),C(3,0).经过A,B,C向x轴作垂线,分别交抛物线组y1,y2,y3,…,yn于A1,B1,C1;A2,B2,C2;A3,B3,C3;…;An,Bn,Cn.记S△A1B1C1为S1,S△A2B2C2为S2,…,S△AnBnCn为Sn,试求S1+S2+S3+…+S10的值.
(4)在(3)问条件下,当n>10时有Sn-10+Sn-9+Sn-8+…Sn的值不小于
,请探求此条件下正整数n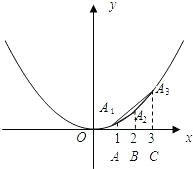 是否存在最大值?若存在,请求出此值;若不存在,请说明理由.
查看习题详情和答案>>
是否存在最大值?若存在,请求出此值;若不存在,请说明理由.
查看习题详情和答案>>
| 1 |
| 4 |
(2)若将(1)问中的抛物线改为y=
| 1 |
| 4 |
| 1 |
| 2 |
(3)现有一抛物线组:y1=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 12 |
| 1 |
| 25 |
| 1 |
| 20 |
| 1 |
| 42 |
| 1 |
| 30 |
| 1 |
| 63 |
(4)在(3)问条件下,当n>10时有Sn-10+Sn-9+Sn-8+…Sn的值不小于
| 11 |
| 242 |
 是否存在最大值?若存在,请求出此值;若不存在,请说明理由.
查看习题详情和答案>>
是否存在最大值?若存在,请求出此值;若不存在,请说明理由.
查看习题详情和答案>>
(1)如图1,抛物线y=ax2(a≠0)的顶点为P,C、D是抛物线上的两点,CA、DB分别垂直于x轴,垂足为A、B,且PA=AB,若点A的横坐标为b,在直线PC上是否存在一点M,使得△MBD是以BD为底的等腰三角形?若存在,求出点M的坐标;若不存在,说明理由;
(2)如图2,若将(1)中“抛物线y=ax2(a≠0)”改为“抛物线y=ax2-2amx+am2(a≠0)”,其他条件不变,试探究(1)中的问题.
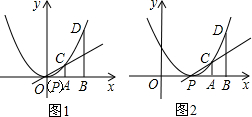 查看习题详情和答案>>
查看习题详情和答案>>
(2)如图2,若将(1)中“抛物线y=ax2(a≠0)”改为“抛物线y=ax2-2amx+am2(a≠0)”,其他条件不变,试探究(1)中的问题.
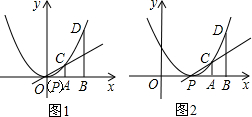 查看习题详情和答案>>
查看习题详情和答案>>
(1)如图1,抛物线y=ax2(a≠0)的顶点为P,C、D是抛物线上的两点,CA、DB分别垂直于x轴,垂足为A、B,且PA=AB,若点A的横坐标为b,在直线PC上是否存在一点M,使得△MBD是以BD为底的等腰三角形?若存在,求出点M的坐标;若不存在,说明理由;
(2)如图2,若将(1)中“抛物线y=ax2(a≠0)”改为“抛物线y=ax2-2amx+am2(a≠0)”,其他条件不变,试探究(1)中的问题.
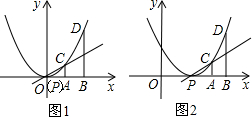
查看习题详情和答案>>
(1)如图1,抛物线y=ax2(a≠0)的顶点为P,C、D是抛物线上的两点,CA、DB分别垂直于x轴,垂足为A、B,且PA=AB,若点A的横坐标为b,在直线PC上是否存在一点M,使得△MBD是以BD为底的等腰三角形?若存在,求出点M的坐标;若不存在,说明理由;
(2)如图2,若将(1)中“抛物线y=ax2(a≠0)”改为“抛物线y=ax2-2amx+am2(a≠0)”,其他条件不变,试探究(1)中的问题.
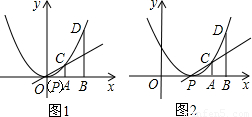
查看习题详情和答案>>
(2)如图2,若将(1)中“抛物线y=ax2(a≠0)”改为“抛物线y=ax2-2amx+am2(a≠0)”,其他条件不变,试探究(1)中的问题.
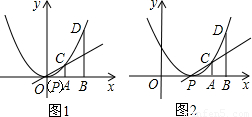
查看习题详情和答案>>

 (一)如图,放在直角坐标系中的正方形ABCD的边长为4.现做如下实验:
(一)如图,放在直角坐标系中的正方形ABCD的边长为4.现做如下实验: ?若存在,指出其中的一种平移方式;若不存在,请说明理由;
?若存在,指出其中的一种平移方式;若不存在,请说明理由;