摘要:(2) 设是原方程组的一个解.求m的值,
网址:http://m.1010jiajiao.com/timu_id_674786[举报]
已知关于x、y的方程组
(1) 把方程(2)化为两个二元一次方程;
(2) 设![]() (k>0)是原方程组的一个解.求m的值;
(k>0)是原方程组的一个解.求m的值;
(3) 若 (ab<0)和
(ab<0)和 (cd<0)是原方程组的两个解,并且
(cd<0)是原方程组的两个解,并且![]() ,求m的值.
,求m的值.
(2005•遵义)已知关于x的一元二次方程x2+(2k-1)x+k2=0
(1)若原方程有两个不相等的实数根,求k的取值范围;
(2)设x1,x2是原方程的两个实数根,且
+
=17,求k的值.
查看习题详情和答案>>
(1)若原方程有两个不相等的实数根,求k的取值范围;
(2)设x1,x2是原方程的两个实数根,且
| x | 2 1 |
| x | 2 2 |
检验方程组的解时,必须将求得的未知数的值代入方程组中的每一个方程.
例1:解方程组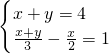
思路分析:本例这两个方程中①较简单,且x、y的系数均为1,故可把①变形,把x用y表示,或把y用x来表示皆可,然后将其代入②,消去一个未知数,化成一元一次方程,进而再求出方程组的解.
解:把①变形为y=4-x ③
把③代入②得: -
- =1
=1
即 -
- =1,
=1, =
= -1,
-1, =
=
∴x=
把x= 代入③得y=4-
代入③得y=4- =3
=3
所以原方程的解是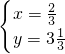 .
.
若想知道解的是否正确,可作如下检验:
检验:把x= ,y=3
,y=3 代入①得,左边=x+y=
代入①得,左边=x+y= +3
+3 =4,右边=4.
=4,右边=4.
所以左边=右边.
再把x= ,y=3
,y=3 代入②得
代入②得
左边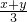 -
- =
=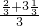 -
-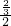 =
= -
- =1,右边=1.
=1,右边=1.
所以左边=右边.
所以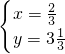 是原方程组的解.
是原方程组的解.
查看习题详情和答案>>
检验方程组的解时,必须将求得的未知数的值代入方程组中的每一个方程.
例1:解方程组
思路分析:本例这两个方程中①较简单,且x、y的系数均为1,故可把①变形,把x用y表示,或把y用x来表示皆可,然后将其代入②,消去一个未知数,化成一元一次方程,进而再求出方程组的解.
把①变形为y=4-x ③
把③代入②得:
-
=1
即
-
=1,
=
-1,
=
∴x=
把x=
代入③得y=4-
=3
所以原方程的解是
.
若想知道解的是否正确,可作如下检验:
检验:把x=
,y=3
代入①得,左边=x+y=
+3
=4,右边=4.
所以左边=右边.
再把x=
,y=3
代入②得
左边
-
=
-
=
-
=1,右边=1.
所以左边=右边.
所以
是原方程组的解.
查看习题详情和答案>>
例1:解方程组
|
思路分析:本例这两个方程中①较简单,且x、y的系数均为1,故可把①变形,把x用y表示,或把y用x来表示皆可,然后将其代入②,消去一个未知数,化成一元一次方程,进而再求出方程组的解.
把①变形为y=4-x ③
把③代入②得:
| x+4-x |
| 3 |
| x |
| 2 |
即
| 4 |
| 3 |
| x |
| 2 |
| x |
| 2 |
| 4 |
| 3 |
| x |
| 2 |
| 1 |
| 3 |
∴x=
| 2 |
| 3 |
把x=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
所以原方程的解是
|
若想知道解的是否正确,可作如下检验:
检验:把x=
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
所以左边=右边.
再把x=
| 2 |
| 3 |
| 1 |
| 3 |
左边
| x+y |
| 3 |
| x |
| 2 |
| ||||
| 3 |
| ||
| 2 |
| 4 |
| 3 |
| 1 |
| 3 |
所以左边=右边.
所以
|
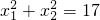 ,求k的值.
,求k的值.