摘要：24．如图①.E.F.M.N是正方形ABCD四条边AB.BC.CD.DA上可以移动的四个点.每组对边上的两个点.可以连接成一条线段．(1)如图②.如果EF//BC. MN//CD.那么EF MN.EF MN,(2)如图③.如果E与A.F与C.M与B.N与D重合.那么EF MN,EF MN
网址：http://m.1010jiajiao.com/timu_id_672029[举报]
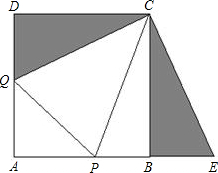如图，正方形ABCD（四个角都是直角，四条边都相等）的边长为1，AB，AD上各有一点P、Q，△APQ的周长为2，求∠PCQ．为了解决这个问题，我们在正方形外以BC和AB的延长线为边作△CBE，使得△CBE≌△CDQ．（1）△CBE可以看成是由△CDQ怎样运动变化得到的？请你描述这一运动变化；
（2）图中PQ与PE的长度是相等的．请你说明理由；
（3）请用（1）或（2）中的结论说明△PCQ≌△PCE；
（4）请用以上的结论，求∠PCQ的度数． 查看习题详情和答案>>
如图，在梯形ABCD中，AD∥BC，若E，F，G，H分别是梯形ABCD各边AB、BC、CD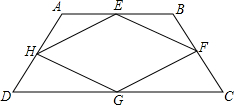
、DA的中点．
（1）求证：四边形EFGH平行四边形；
（2）当梯形ABCD满足什么条件时，四边形EFGH是菱形；
（3）在（2）的条件下，梯形ABCD满足什么条件时，四边形EFGH是正方形． 查看习题详情和答案>>
、DA的中点．（1）求证：四边形EFGH平行四边形；
（2）当梯形ABCD满足什么条件时，四边形EFGH是菱形；
（3）在（2）的条件下，梯形ABCD满足什么条件时，四边形EFGH是正方形． 查看习题详情和答案>>
如图，正方形ABCD中，E、F是对角线AC上两点，连接BE、BF、DE、DF，则添加下列条件①∠ABE=∠CBF；②AE=CF；③AB=AF；④BE=BF．可以判定四边形BEDF是菱形的条件有（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
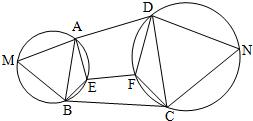22、如图，四边形ABCD中，△ABM，△CDN是分别以AB、CD为一条边的正三角形，E、F分别在这二个三角形外接圆上，试问AE+EB+EF+FD+FC是否存在最小值？若存在最小值，则E、F两点的位置在什么地方？并说明理由．若不存在最小值，亦请说出理由．
6、如图，四边形ABCD是正方形，E是CD边的中点，P是BC边上的一动点，下列条件中，不能推出△ABP与△ECP相似的是（ ）