摘要：如图.在梯形ABCD中.AB∥DC.∠BCD=90°.且AB=1.BC=2.tan∠ADC=2．(1)求证:DC=BC, (2)E是梯形内的一点.F是梯形外的一点.．且∠EDC=∠FBC.DE=BF.试判断△ECF的形状.并证明你的结论,的条件下.当BE:CE=1:2.∠BEC=135°时.求sin∠BFE的值．
网址：http://m.1010jiajiao.com/timu_id_666772[举报]
如图，在梯形ABCD中，AB∥DC，∠BCD=90°，且AB=1，BC=2，tan∠ADC=2．
（1）求证：DC=BC；
（2）E是梯形内一点，F是梯形外一点，且∠EDC=∠FBC，DE=BF，试判断△ECF的形状，并证明你的结论．
查看习题详情和答案>>
如图，在梯形ABCD中，AB∥DC，∠BCD=90°，且AB=1，BC=2，tan∠ADC=2．
（1）求证：DC=BC；
（2）E是梯形内一点，F是梯形外一点，且∠EDC=∠FBC，DE=BF，试判断△ECF的形状，并证明你的结论．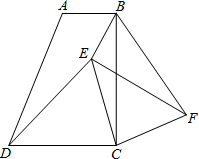
查看习题详情和答案>>
（1）求证：DC=BC；
（2）E是梯形内一点，F是梯形外一点，且∠EDC=∠FBC，DE=BF，试判断△ECF的形状，并证明你的结论．
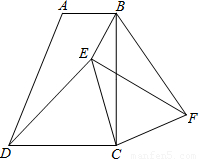
如图，在梯形ABCD中，AB∥DC，∠BCD=90°，且AB=1，BC=2，tan∠ADC=2．
（1）求证：DC=BC；
（2）E是梯形内一点，F是梯形外一点，且∠EDC=∠FBC，DE=BF，试判断△ECF的形状，并证明你的结论．
查看习题详情和答案>>
（1）求证：DC=BC；
（2）E是梯形内一点，F是梯形外一点，且∠EDC=∠FBC，DE=BF，试判断△ECF的形状，并证明你的结论．
查看习题详情和答案>>
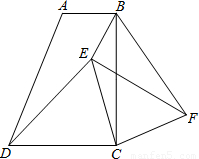
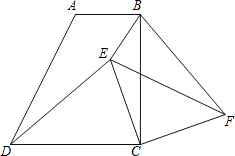如图，在梯形ABCD中，AB∥CD，∠BCD=90°，且AB=1，BC=2，tan∠ADC=2．