摘要：解:∵∠1=∠2∠2=∠5( )∴∠1=∠5∴ ∥ ( )∴∠3+∠4=180°( )∵∠3=105°∴∠4=
网址：http://m.1010jiajiao.com/timu_id_665941[举报]
19、已知：如图 AD∥CB，∠A=∠C，若∠ABD=32°，求∠BDC的度数．有同学用了下面的方法．但由于一时犯急没有写完整，请你帮他添写完整．
解：∵AD∥CB （已知）
∴∠C+∠ADC=180°（
两直线平行，同旁内角互补
）又∵∠A=∠C （已知）
∴∠A+∠ADC=180°（等量代换）
∴AB∥CD （
同旁内角互补，两直线平行
）∴∠BDC=
∠DBA
=32
°（
两直线平行，内错角相等
）．
23、已知：如图，AB∥CD，∠A=∠D，试说明 AC∥DE 成立的理由．（下面是彬彬同学进行的推理，请你将彬彬同学的推理过程补充完整．）
解：∵AB∥CD （已知）
∴∠A=
∠ACD
（两直线平行，内错角相等）又∵∠A=∠D（
已知
）∴∠
ACD
=∠D
（等量代换）∴AC∥DE （
内错角相等，两直线平行
）
已知，如图，BE平分∠ABC，DE∥BC，∠3=35°，求∠1的度数解：因为BE平分∠ABC（已知）
所以
∠1=∠2
∠1=∠2
（ 角平分线意义）因为DE∥BC（ 已知）
所以
∠2=∠3
∠2=∠3
（
两直线平行，内错角相等
两直线平行，内错角相等
）所以
∠1=∠3
∠1=∠3
（
等量代换
等量代换
）因为∠3=35°（ 已知）
所以∠1=
35°
35°
°．
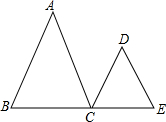已知：如图，AB∥CD，∠A=∠D，试说明 AC∥DE 成立的理由．