摘要:28.小明对下列各式进行计算的结果如下: 1+3=4=22 1+3+5=9=32 1+3+5+7=16=42 1+3+5+7+9=25=52.(1)根据小明计算的结果.你认为下式的结果应是谁的平方? 1+3+5+7+-+29= .
网址:http://m.1010jiajiao.com/timu_id_665423[举报]
 (2012•贵阳模拟)阅读下列材料:
(2012•贵阳模拟)阅读下列材料:已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=-
| 2 | x |
(1)若P点坐标为(1,0),请你写出:M的坐标是
(2,-1)
(2,-1)
;(2)若点P的坐标为(m,0),求直线M1M的函数关系式.
阅读下列材料:
已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=- 的图象上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形一定有两个,如图所示,并且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
的图象上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形一定有两个,如图所示,并且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
(1)若P点坐标为(1,0),请你写出:M的坐标是______;
(2)若点P的坐标为(m,0),求直线M1M的函数关系式.
 查看习题详情和答案>>
查看习题详情和答案>>
已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=-
 的图象上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形一定有两个,如图所示,并且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
的图象上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形一定有两个,如图所示,并且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.(1)若P点坐标为(1,0),请你写出:M的坐标是______;
(2)若点P的坐标为(m,0),求直线M1M的函数关系式.
 查看习题详情和答案>>
查看习题详情和答案>>
在计算某一样本:12,16,11,…的方差时,小明按以下算式进行计算:S2=
[(12-20)2+(16-20)2+(-6-20)2+(11-20)2+…],则计算式中数字14和20分别表示样本中的( )
| 1 |
| 14 |
查看习题详情和答案>>
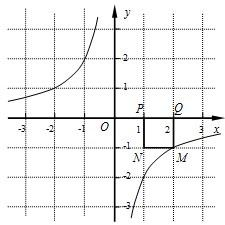 已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=-
已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=-| 2 |
| x |
(1)如图所示,若反比例函数解析式为y=-
| 2 |
| x |
(2)请你通过改变P点坐标,对直线M1M的解析式y﹦kx+b进行探究可得k﹦
(3)依据(2)的规律,如果点P的坐标为(6,0),请你求出点M1和点M的坐标. 查看习题详情和答案>>
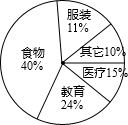 (2012•瑶海区一模)在春节期间,小明对自己家7天的家庭开支情况进行了统计,各类支出如图所示,用于食物费用为800元,那么本月用于教育的费用为( )
(2012•瑶海区一模)在春节期间,小明对自己家7天的家庭开支情况进行了统计,各类支出如图所示,用于食物费用为800元,那么本月用于教育的费用为( )