摘要:⑶当点在线段上滑动时.是否可能成为等腰三角形?如果可能.指出所有能使成为等腰三角形的点的位置.并求出相应的的值,如果不可能.试说明理由.(图⑷.图⑸.图⑹的的形状.大小相同.图⑷供操作.实验用.图⑸和图⑹备用)
网址:http://m.1010jiajiao.com/timu_id_660537[举报]
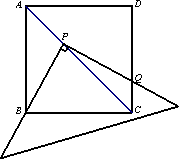
操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.
探究:设A,P两点间的距离为x.当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应的x的值;如果不可能,试说明理由.
如图1,在平面直角坐标系xOy中,直线y1=-x上一点A(-1,1),过点A作AB⊥x轴于B.在图中画图探究:将一把三角尺的直角顶点P放在线段AO上滑行,直角的一边始终经过点B,另一边与y轴相交于点Q.
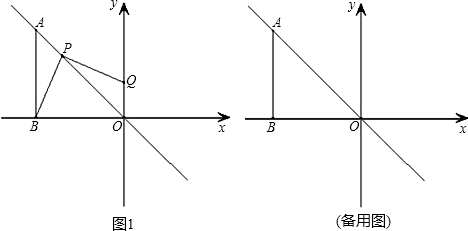
(1)判断线段PQ与线段PB的数量关系,就点P运动到图1所示位置时证明你的结论;
(2)当点P在线段AO上滑行时,△POQ是否可能成为等腰三角形,如果可能,求出所有能使△POQ成为等腰三角形的点P的坐标;如果不可能,请说明理由;
(3)猜想OB、OQ与OP之间的数量关系: .
查看习题详情和答案>>

(1)判断线段PQ与线段PB的数量关系,就点P运动到图1所示位置时证明你的结论;
(2)当点P在线段AO上滑行时,△POQ是否可能成为等腰三角形,如果可能,求出所有能使△POQ成为等腰三角形的点P的坐标;如果不可能,请说明理由;
(3)猜想OB、OQ与OP之间的数量关系: