网址:http://m.1010jiajiao.com/timu_id_654442[举报]
若M![]() 、N
、N![]() 、P
、P![]() 三点都在函数y=
三点都在函数y=![]() (k<0)的图像上,则y1、y2、y3的大小关系为
(k<0)的图像上,则y1、y2、y3的大小关系为
A.y2>y3>y1
B.y2>y1>y3
C.y3>y1>y2"
D.y3>y2>y1
反比例函数y=![]() (k≠0)任取一点M(a,b),过M作MA⊥x轴,MB⊥y轴,所得矩形OAMB的面积为S=MA·MB=|b|·|a|=|ab|.又因为b=
(k≠0)任取一点M(a,b),过M作MA⊥x轴,MB⊥y轴,所得矩形OAMB的面积为S=MA·MB=|b|·|a|=|ab|.又因为b=![]() ,故ab=k,所以S=|k|(如图(1)).
,故ab=k,所以S=|k|(如图(1)).
这就是说,过双曲线上任意一点作x轴、y轴的垂线,所得的矩形面积为|k|.这就是k的几何意义,会给解题带来方便.现举例如下:
例1:如(2)图,已知点P1(x1,y1)和P2(x2,y2)都在反比例函数y=![]() (k<0)的图像上,试比较矩形P1AOB与矩形P2COD的面积大小.
(k<0)的图像上,试比较矩形P1AOB与矩形P2COD的面积大小.
解答:![]() =|k|
=|k|
![]() =|k|
=|k|
故![]() =
=![]()

例2:如图(3),在y=![]() (x>0)的图像上有三点A、B、C,经过三点分别向x轴引垂线,交x轴于A1、B1、C1三点,连结OA、OB、OC,记△OAA1、△OBB1、△OCC1的面积分别为S1、S2、S3,则有( )
(x>0)的图像上有三点A、B、C,经过三点分别向x轴引垂线,交x轴于A1、B1、C1三点,连结OA、OB、OC,记△OAA1、△OBB1、△OCC1的面积分别为S1、S2、S3,则有( )

A.S1=S2=S3
B.S1<S2<S3
C.S3<S1<S2
D.S1>S2>S3
解答:∵![]() =
=![]() |k|=
|k|=![]() ,
,
![]() =
=![]() |k|=
|k|=![]()
![]() =
=![]() |k|=
|k|=![]()
S1=S2=S3,故选A.
例3:一个反比例函数在第三象限的图像如图(4)所示,若A是图像任意一点,AM⊥x轴,垂足为M,O是原点,如果△AOM的面积是3,那么这个反比例函数的解析式是________.

解答:∵S△AOM=![]() |k|
|k|
又S△AOM=3,
∴![]() |k|=3,|k|=6
|k|=3,|k|=6
∴k=±6
又∵曲线在第三象限
∴k>0∴k=6
∴所以反比例函数的解析式为y=![]() .
.
根据是述意义,请你解答下题:
如图(5),过反比例函数y=![]() (x>0)的图像上任意两点A、B分别作轴和垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,比较它们的大小,可得
(x>0)的图像上任意两点A、B分别作轴和垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,比较它们的大小,可得

A.S1>S2
B.S1=S2
C.S1<S2
D.大小关系不能确定
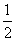 ,y1),N(-
,y1),N(- ,y2),P(
,y2),P( ,y3)三点都在反比例函数y=
,y3)三点都在反比例函数y=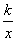 (k<0)的图像上,则y1,y2,y3的大小关系是( )。
(k<0)的图像上,则y1,y2,y3的大小关系是( )。