摘要:(2)在边长为()的正方形中.设黑色小正方形的个数为.白色小正方形的个数为.问是否存在偶数.使?若存在.请写出的值,若不存在.请说明理由.
网址:http://m.1010jiajiao.com/timu_id_653106[举报]
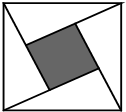 “赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形.如图,是一“赵爽弦图”飞镖板,其直角三角形的短直角边的长为1.这直角三角形都用很细的金属丝围成,飞镖不会扎在这些金属丝上.小明同学距飞镖板一定距离向飞镖板投掷飞镖(假设投掷的飞镖均扎在飞镖板上),则投掷一次飞镖扎在中间小正方形黑色区域的概率是
“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形.如图,是一“赵爽弦图”飞镖板,其直角三角形的短直角边的长为1.这直角三角形都用很细的金属丝围成,飞镖不会扎在这些金属丝上.小明同学距飞镖板一定距离向飞镖板投掷飞镖(假设投掷的飞镖均扎在飞镖板上),则投掷一次飞镖扎在中间小正方形黑色区域的概率是| 1 | 5 |
(1)求直角三角形的长直角边的长;
(2)连续以同样的要求向飞镖板投掷两支飞镖,求投中位置为一黑一白的概率.(请结合树状图或列表加以解答) 查看习题详情和答案>>
 “赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形.如图,是一“赵爽弦图”飞镖板,其直角三角形的短直角边的长为1.这直角三角形都用很细的金属丝围成,飞镖不会扎在这些金属丝上.小明同学距飞镖板一定距离向飞镖板投掷飞镖(假设投掷的飞镖均扎在飞镖板上),则投掷一次飞镖扎在中间小正方形黑色区域的概率是
“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形.如图,是一“赵爽弦图”飞镖板,其直角三角形的短直角边的长为1.这直角三角形都用很细的金属丝围成,飞镖不会扎在这些金属丝上.小明同学距飞镖板一定距离向飞镖板投掷飞镖(假设投掷的飞镖均扎在飞镖板上),则投掷一次飞镖扎在中间小正方形黑色区域的概率是 .
.
(1)求直角三角形的长直角边的长;
(2)连续以同样的要求向飞镖板投掷两支飞镖,求投中位置为一黑一白的概率.(请结合树状图或列表加以解答)
查看习题详情和答案>>
“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形.如图,是一“赵爽弦图”飞镖板,其直角三角形的短直角边的长为1.这直角三角形都用很细的金属丝围成,飞镖不会扎在这些金属丝上.小明同学距飞镖板一定距离向飞镖板投掷飞镖(假设投掷的飞镖均扎在飞镖板上),则投掷一次飞镖扎在中间小正方形黑色区域的概率是 .
.
(1)求直角三角形的长直角边的长;
(2)连续以同样的要求向飞镖板投掷两支飞镖,求投中位置为一黑一白的概率.(请结合树状图或列表加以解答)
 查看习题详情和答案>>
查看习题详情和答案>>
 .
.(1)求直角三角形的长直角边的长;
(2)连续以同样的要求向飞镖板投掷两支飞镖,求投中位置为一黑一白的概率.(请结合树状图或列表加以解答)
 查看习题详情和答案>>
查看习题详情和答案>>
如图6所示,正方形ABCD的边长为12,划分成12×12个小正方形格,将边长为n(n为整数,且2≤n≤11)的黑白两色正方形纸片按图中的方式,黑白相间地摆放,第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格,第二张纸片盖住第一张纸片的部分恰好为(n-1)×(n-1)个小正方形.如此摆放下去,直到纸片盖住正方形ABCD的右下角为止.
请你认真观察思考后回答下列问题:
(1)由于正方形纸片边长n的取值不同,完成摆放时所使用正方形纸片的张数也不同,请填写下表:
| 纸片的边长n | 2 | 3 | 4 | 5 | 6 |
| 使用的纸片张数 |
(2)设正方形ABCD被纸片盖住的面积(重合部分只计一次)为S1,未被盖住的面积为S2.
①当n=2时,求S1∶S2的值;
②是否存在使得S1=S2的n值?若存在,请求出来;若不存在,请说明理由.
 |
查看习题详情和答案>>

