网址:http://m.1010jiajiao.com/timu_id_61964[举报]
1
11. .files/image318.gif) . 12.
. 12..files/image320.gif) 13.
13. .files/image322.gif) 14. 60 15. ①③
14. 60 15. ①③
16.解:(Ⅰ)∵.files/image324.gif) -
-
.files/image326.gif)
∴.files/image328.gif) ,(3分)
,(3分)
∴.files/image330.gif)
又已知点.files/image332.gif) 为
为.files/image334.gif) 的图像的一个对称中心。∴
的图像的一个对称中心。∴.files/image336.gif)
而.files/image338.gif) (6分)
(6分)
(Ⅱ)若.files/image340.gif) ,
,
.files/image342.gif) (9分)
(9分)
∵.files/image344.gif)
.files/image346.gif) ,∴
,∴.files/image348.gif)
即m的取值范围是.files/image350.gif) (12分)
(12分)
17. 解:(1)由已知得.files/image352.gif) ,∵
,∵.files/image253.gif) ,∴
,∴.files/image355.gif)
∵.files/image245.gif) 、
、.files/image247.gif) 是方程
是方程.files/image251.gif) 的两个根,∴
的两个根,∴.files/image360.gif)
∴.files/image362.gif) ,
,.files/image364.gif) ………………6分
………………6分
(2).files/image255.gif) 的可能取值为0,100,200,300,400
的可能取值为0,100,200,300,400
.files/image367.gif) ,
,.files/image369.gif) ,
,
.files/image371.gif) ,
,.files/image373.gif) ,
,
.files/image375.gif) 即
即.files/image255.gif) 的分布列为:
的分布列为:
.files/image255.gif)
.files/image234.gif)
.files/image238.gif)
.files/image242.gif)
.files/image380.gif)
.files/image382.gif)
.files/image090.gif)
.files/image385.gif)
.files/image387.gif)
.files/image389.gif)
.files/image389.gif)
.files/image387.gif)
故.files/image393.gif) ………12分
………12分
18解法一:
(1)延长C
.files/image395.jpg) 所以F为C1N的中点,B为CN的中点。????2分
所以F为C1N的中点,B为CN的中点。????2分
又M是线段AC1的中点,故MF∥AN。?????3分
又MF.files/image397.gif) 平面ABCD,AN
平面ABCD,AN.files/image399.gif) 平面ABCD。
平面ABCD。
∴MF∥平面ABCD。 ???5分
(2)证明:连BD,由直四棱柱ABCD―A1B
可知A.files/image401.gif) 平面ABCD,
平面ABCD,
∴A
又∵AC∩A.files/image401.gif) 平面ACC
平面ACC
∴BD⊥平面ACC
在四边形DANB中,DA∥BN且DA=BN,所以四边形DANB为平行四边形
故NA∥BD,∴NA⊥平面ACC.files/image401.gif) 平面AFC1
平面AFC1
∴平面AFC1⊥ACC
(3)由(2)知BD⊥ACC.files/image401.gif) ACC
ACC
又由BD⊥AC可知NA⊥AC,
∴∠C
在Rt△C.files/image404.gif) ,故∠C
,故∠C
∴平面AFC1与平面ABCD所成二面角的大小为30°或150°。???12分
19.解:(Ⅰ)因为.files/image262.gif) 成等差数列,点
成等差数列,点.files/image264.gif) 的坐标分别为
的坐标分别为.files/image266.gif) 所以
所以.files/image406.gif) 且
且.files/image408.gif)
由椭圆的定义可知点.files/image268.gif) 的轨迹是以
的轨迹是以.files/image264.gif) 为焦点长轴为4的椭圆(去掉长轴的端点),
为焦点长轴为4的椭圆(去掉长轴的端点),
所以.files/image410.gif) .故顶点
.故顶点.files/image268.gif) 的轨迹
的轨迹.files/image270.gif) 方程为
方程为.files/image412.gif) .…………4分
.…………4分
(Ⅱ)由题意可知直线.files/image414.gif) 的斜率存在,设直线
的斜率存在,设直线.files/image414.gif) 方程为
方程为.files/image416.gif) .
.
由.files/image418.gif) 得
得.files/image420.gif) ,
,
设.files/image422.gif) 两点坐标分别为
两点坐标分别为.files/image424.gif) ,则
,则.files/image426.gif) ,
,
.files/image428.gif) ,所以线段CD中点E的坐标为
,所以线段CD中点E的坐标为.files/image430.gif) ,故CD垂直平分线l的方程为
,故CD垂直平分线l的方程为.files/image432.gif) ,令y=0,得
,令y=0,得.files/image092.gif) 与
与.files/image283.gif) 轴交点的横坐标为
轴交点的横坐标为.files/image434.gif) ,由
,由.files/image278.gif) 得
得.files/image436.gif) ,解得
,解得.files/image438.gif) ,
,
又因为.files/image440.gif) ,所以
,所以.files/image442.gif) .当
.当.files/image438.gif) 时,有
时,有.files/image444.gif) ,此时函数
,此时函数.files/image446.gif) 递减,所以
递减,所以.files/image448.gif) .所以,
.所以,.files/image450.gif) .
.
故直线.files/image092.gif) 与
与.files/image283.gif) 轴交点的横坐标的范围是
轴交点的横坐标的范围是.files/image452.gif) .
………………12分
.
………………12分
20.解:(1)因为.files/image454.gif)
所以设S=.files/image456.gif)
.files/image458.gif) (1)
(1)
S=.files/image460.gif) ……….(2)(1)+(2)得:
……….(2)(1)+(2)得:
.files/image462.gif) =
=.files/image464.gif) , 所以S=3012
, 所以S=3012
(2)由.files/image293.gif) 两边同减去1,得
两边同减去1,得.files/image466.gif)
所以.files/image468.gif) ,
,
所以.files/image470.gif) ,
,.files/image472.gif) 是以2为公差以
是以2为公差以.files/image474.gif) 为首项的等差数列,
为首项的等差数列,
所以.files/image476.gif)
.files/image478.gif)
(3)因为.files/image480.gif)
所以.files/image482.gif)
.files/image484.gif)
所以.files/image486.gif)
>.files/image488.gif)
21.解:(1)∵ .files/image490.gif) ∴
∴.files/image492.gif) …1分
…1分
设.files/image494.gif)
.files/image496.gif) 则
则.files/image498.gif) ……2分
……2分
∴.files/image500.gif) 在
在.files/image301.gif) 上为减函数 又
上为减函数 又.files/image503.gif)
.files/image505.gif) 时,
时,.files/image500.gif)
.files/image507.gif) ,
,
∴.files/image509.gif) ∴
∴.files/image299.gif) 在
在.files/image301.gif) 上是减函数………4分(2)①
上是减函数………4分(2)①
∵.files/image513.gif) ∴
∴.files/image515.gif) 或
或.files/image517.gif) 时
时
.files/image519.gif) ∴
∴.files/image521.gif) …………………………………6分
…………………………………6分
.files/image303.gif) 又≤
又≤.files/image174.gif) ≤
≤.files/image306.gif) 对一切
对一切.files/image308.gif) 恒成立 ∴
恒成立 ∴.files/image303.gif) ≤
≤.files/image174.gif) ≤
≤.files/image529.gif) ……………8分
……………8分
②显然当.files/image531.gif) 或
或.files/image533.gif) 时,不等式成立
…………………………9分
时,不等式成立
…………………………9分
当.files/image535.gif) ,原不等式等价于
,原不等式等价于.files/image537.gif) ≥
≥.files/image539.gif) ………10分
………10分
下面证明一个更强的不等式:.files/image537.gif) ≥
≥.files/image541.gif) …①
…①
即.files/image543.gif) ≥
≥.files/image545.gif) ……②亦即
……②亦即.files/image547.gif) ≥
≥.files/image549.gif) …………………………11分
…………………………11分
由(1) 知.files/image549.gif) 在
在.files/image552.gif) 上是减函数 又
上是减函数 又.files/image554.gif) ∴
∴.files/image556.gif) ……12分
……12分
∴不等式②成立,从而①成立 又.files/image558.gif)
.files/image539.gif)
∴.files/image537.gif) >
>.files/image539.gif)
综合上面∴.files/image234.gif) ≤
≤.files/image283.gif) ≤
≤.files/image312.gif) 且
且.files/image234.gif) ≤
≤.files/image174.gif) ≤
≤.files/image040.gif) 时,原不等式成立 ……………………………14分
时,原不等式成立 ……………………………14分
本资料由《七彩教育网》www.7caiedu.cn 提供!
如果我们把形如
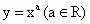 的函数成为幂函数,现已知幂函数
的函数成为幂函数,现已知幂函数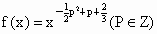 在(0,+∞)上是增函数,且在其定义域内是偶函数.
在(0,+∞)上是增函数,且在其定义域内是偶函数.
(1)
求p的值,并写出相应的函数f(x);(2)
对于(1)中求得的函数f(x),设函数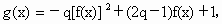 问是否存在实数q(q<0),使得g(x)在区间(-∞,-4]上是减函数,且在(-4,0)上是增函数?若存在,请求出q来,若不存在,请说明理由.
查看习题详情和答案>>
问是否存在实数q(q<0),使得g(x)在区间(-∞,-4]上是减函数,且在(-4,0)上是增函数?若存在,请求出q来,若不存在,请说明理由.
查看习题详情和答案>>
如果我们把形如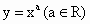 的函数成为幂函数,现已知幂函数
的函数成为幂函数,现已知幂函数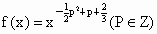 在(0,+∞)上是增函数,且在其定义域内是偶函数.
在(0,+∞)上是增函数,且在其定义域内是偶函数.
(1)求p的值,并写出相应的函数f(x);
(2)对于(1)中求得的函数f(x),设函数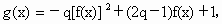 问是否存在实数q(q<0),使得g(x)在区间(-∞,-4]上是减函数,且在(-4,0)上是增函数?若存在,请求出q来,若不存在,请说明理由.
问是否存在实数q(q<0),使得g(x)在区间(-∞,-4]上是减函数,且在(-4,0)上是增函数?若存在,请求出q来,若不存在,请说明理由.
已知函数![]() ,其中
,其中![]()
(1)若![]() 为偶函数,求a的值;
为偶函数,求a的值;
(2)命题p:函数![]() 上是增函数,命题q:函数
上是增函数,命题q:函数![]() 是减函数,如果p或q为真,p且q为假,求a的取值范围。
是减函数,如果p或q为真,p且q为假,求a的取值范围。
(3)在(2)的条件下,比较![]() 的大小。
的大小。