网址:http://m.1010jiajiao.com/timu_id_59848[举报]
一、选择题
1―5 ADBAC 6―10 BCDCD 11―12 AB
二、填空题
13.24 14.24个 15.144 .files/image131.gif) 16.②
16.②
三、解答题
17.解:随机猜对问题A的概率p1=.files/image133.gif) ,随机猜对问题B的概率p2=
,随机猜对问题B的概率p2=.files/image135.gif) .………1分
.………1分
回答问题的顺序有两种,分别讨论如下:
(1)先回答问题A,再回答问题B.
参与者获奖金额ξ可取0,m,m+n.,则
P(ξ=0)=1-p1=.files/image137.gif) ,P(ξ=m)=p1(1-p2)=
,P(ξ=m)=p1(1-p2)=.files/image139.gif) ,P(ξ=m+n)=p1p2=
,P(ξ=m+n)=p1p2=.files/image141.gif) .
.
Eξ=0×.files/image137.gif) +m×
+m×.files/image139.gif) +(m+n)×
+(m+n)×.files/image141.gif) =
=.files/image143.gif) .
………5分
.
………5分
(2)先回答问题B,再回答问题A.
参与者获奖金额η可取0,n,m+n.,则
P(η=0)=1-p2=.files/image145.gif) ,P(η=n)=p2(1-p1)=
,P(η=n)=p2(1-p1)=.files/image147.gif) ,P(η=m+n)=p2p1=
,P(η=m+n)=p2p1=.files/image141.gif) .
.
Eη=0×.files/image145.gif) +n×
+n×.files/image147.gif) +(m+n)×
+(m+n)×.files/image141.gif) =
=.files/image149.gif) .
………9分
.
………9分
Eξ-Eη=(.files/image143.gif) )-(
)-(.files/image149.gif) )=
)=.files/image151.gif)
于是,当.files/image153.gif) >
>.files/image155.gif) 时,Eξ>Eη,先回答问题A,再回答问题B,获奖的期望值较大;
时,Eξ>Eη,先回答问题A,再回答问题B,获奖的期望值较大;
当.files/image153.gif) =
=.files/image155.gif) 时,Eξ=Eη,两种顺序获奖的期望值相等;
时,Eξ=Eη,两种顺序获奖的期望值相等;
当.files/image153.gif) <
<.files/image155.gif) 时,Eξ<Eη,先回答问题B,再回答问题A,获奖的期望值较大. ………12分
时,Eξ<Eη,先回答问题B,再回答问题A,获奖的期望值较大. ………12分
18.解:(1).files/image157.gif)
.files/image159.gif) ………3分
………3分
∵角A为钝角,
.files/image161.gif) ……………………………4分
……………………………4分
.files/image163.gif) 取值最小值,
取值最小值,
其最小值为.files/image165.gif) ……………………6分
……………………6分
(2)由.files/image167.gif) ………………8分
………………8分
.files/image169.gif) ,
,
.files/image171.gif) …………10分
…………10分
在△.files/image173.gif) 中,由正弦定理得:
中,由正弦定理得:.files/image175.gif) ……12分
……12分
19.(Ⅰ)证法一:取.files/image177.gif) 的中点G,连结FG、AG,
的中点G,连结FG、AG,
依题意可知:GF是.files/image179.gif) 的中位线,
的中位线,
则
GF∥.files/image181.gif) 且
且.files/image183.gif) ,
,
AE∥.files/image181.gif) 且
且.files/image185.gif) ,
,
所以GF∥AE,且GF=AE,即四边形AEFG为平行四边形,………3分
则EF∥AG,又AG.files/image187.gif) 平面
平面.files/image189.gif) ,EF
,EF.files/image191.gif) 平面
平面.files/image189.gif) ,
,
所以EF∥平面.files/image189.gif) .
………6分
.
………6分
证法二:取DC的中点G,连结FG,GE.
∵.files/image193.gif) ∥
∥.files/image177.gif) ,
,.files/image196.gif) 平面
平面.files/image189.gif) ,∴FG∥平面
,∴FG∥平面.files/image189.gif) .
.
同理:.files/image199.gif) ∥平面
∥平面.files/image189.gif) ,且
,且.files/image201.gif) ,
,
∴平面EFG∥平面.files/image189.gif) ,
………3分
,
………3分
.files/image203.gif) 平面
平面.files/image205.gif) ,
,
∴EF∥平面.files/image189.gif) .
………6分
.
………6分
证法三:连结EC延长交AD于K,连结.files/image207.gif) ,E、F分别CK、CD1的中点,
,E、F分别CK、CD1的中点,
所以 FE∥D1K ………3分
∵FE∥D1K,.files/image209.gif) 平面
平面.files/image189.gif) ,
,.files/image211.gif)
.files/image191.gif) 平面
平面.files/image189.gif) ,∴EF∥平面
,∴EF∥平面.files/image189.gif) .
………6分
.
………6分
(Ⅱ)解法一:.files/image214.gif) ⊥平面ABCD,过D在平面ABCD内作DH⊥EC于H,连接D1H.
⊥平面ABCD,过D在平面ABCD内作DH⊥EC于H,连接D1H.
∵DH是D1H在平面ABCD内的射影,∴D1H⊥EC.
∴∠DHD1为二面角.files/image216.gif) 的平面角。即∠DHD1=
的平面角。即∠DHD1=.files/image218.gif) .
………8分
.
………8分
在△DHD1中,tan∠DHD1=.files/image220.gif) ,∴
,∴.files/image222.gif) ,
,.files/image224.gif) =
=.files/image226.gif) ,
,
∴.files/image228.gif) ,∴
,∴.files/image230.gif) ,∴
,∴.files/image232.gif) ,∴
,∴.files/image234.gif) . ………12分
. ………12分
解法二:以D为原点,AD、DC、DD1分别为x、y、z轴建立空间直角坐标系。
D(0,0,0),D1(0,0,1),E(1,x,0)、C(0,2,0)。
平面DEC的法向量.files/image236.gif) =(0,0,1),设
=(0,0,1),设.files/image238.gif) 为平面D1EC的法向量,
为平面D1EC的法向量,
则.files/image240.gif) ∴
∴.files/image242.gif) ∴
∴.files/image244.gif) 。 ………8分
。 ………8分
设二面角.files/image216.gif) 的大小为
的大小为.files/image246.gif) ,∴cos
,∴cos.files/image246.gif) =
=.files/image248.gif)
.files/image250.gif) 。
。
∴.files/image252.gif) ,∴
,∴.files/image254.gif) ∵
∵.files/image256.gif) <2,∴
<2,∴.files/image258.gif) 。
………12分
。
………12分
20.解(Ⅰ)设.files/image260.gif) ,
,.files/image262.gif) ,椭圆的方程为
,椭圆的方程为.files/image264.gif) .
.
∵直线.files/image266.gif) 平行于向量
平行于向量.files/image268.gif) ,
,
∴.files/image268.gif) 与
与.files/image270.gif) =(3,1)共线
=(3,1)共线
∴.files/image272.gif) .
.
∴.files/image274.gif) 。
………2分
。
………2分
又∵.files/image276.gif) 、
、.files/image278.gif) 在椭圆上,∴
在椭圆上,∴.files/image280.gif) ∴
∴.files/image282.gif) ,
,
∴.files/image284.gif) =-1,
………4分
=-1,
………4分
∴.files/image286.gif) ,∴
,∴.files/image288.gif) ,
,.files/image290.gif) ,∴
,∴.files/image292.gif) .………6分
.………6分
(Ⅱ)设.files/image294.gif) ,因为直线AB过
,因为直线AB过.files/image296.gif) (
(.files/image298.gif) ,0),所以直线AB的方程为:
,0),所以直线AB的方程为:.files/image300.gif) ,代入椭圆方程中得
,代入椭圆方程中得
∵.files/image302.gif) ∴
∴.files/image304.gif) ,即
,即.files/image306.gif) ,
,
∴.files/image308.gif) ,
………8分
,
………8分
由.files/image310.gif) ,
,
∴.files/image312.gif)
∵.files/image314.gif) ,
,
∴.files/image316.gif)
∴.files/image318.gif) ,
,
∵.files/image320.gif) ,
,.files/image322.gif) ,
,
又因为.files/image324.gif) ,∴
,∴.files/image326.gif) 。………10分
。………10分
∴.files/image328.gif) ,
,
∴.files/image330.gif) ,即
,即.files/image332.gif) 。
。
∴.files/image334.gif) 的轨迹方程
的轨迹方程.files/image332.gif) .
………12分
.
………12分
21.解:(1)①直线PQ的斜率.files/image337.gif)
.files/image339.gif) ,
,
由.files/image341.gif) ,所以
,所以.files/image343.gif) ,
,
即直线PQ的斜率.files/image337.gif)
.files/image346.gif) .
…………2分
.
…………2分
由.files/image348.gif) ,又
,又.files/image350.gif) ,所以
,所以.files/image352.gif) ,
,
即.files/image354.gif) 图象上任一点切线的斜率k的取值范围为
图象上任一点切线的斜率k的取值范围为.files/image356.gif) .
…………4分
.
…………4分
②.files/image358.gif) .
…………6分
.
…………6分
(2)当.files/image360.gif) ,根据(1)中②的结论,得到存在
,根据(1)中②的结论,得到存在.files/image362.gif)
.files/image364.gif) ,
,.files/image366.gif)
.files/image368.gif) ,使得
,使得
.files/image370.gif) ,
,.files/image372.gif) ,
…………9分
,
…………9分
又.files/image374.gif) 为单调递减函数,所以
为单调递减函数,所以.files/image376.gif) ,即
,即
.files/image378.gif) ,而
,而.files/image380.gif) ,所以
,所以
.files/image382.gif) ,
,
因为.files/image360.gif) ,所以x>0, 1-x>0
,所以x>0, 1-x>0
所以 .files/image385.gif) .
…………12分
.
…………12分
22.证明:(Ⅰ)连接OD,∵OD=OA,∴∠OAD=∠ODA,
∵OC∥AD, ∴∠OAD=∠BOC, ∠DOC=∠ODA.
∴∠DOC=∠BOC,∵OD=OB,OC=OC,
∴△DOC≌△BOC. ∴∠ODC=∠OBC. …………2分
∵BC是⊙O的切线, ∴∠OBC=90°, ∴∠ODC=90°,
∴DC是⊙O的切线. …………5分
(Ⅱ)连接BD, ∵AB是⊙0的直径, ∴∠ADB=90°,∴∠OBC=∠ADB.
∵∠OAD=∠BOC.
∴△ADB∽△OBC. ∴.files/image387.gif) ,
,
∴.files/image389.gif) …………10分
…………10分
23.解:(Ⅰ).files/image391.gif) 的参数方程为
的参数方程为.files/image393.gif) ,
,
即.files/image395.gif) 。
…………5分
。
…………5分
(Ⅱ)由.files/image397.gif)
可将.files/image399.gif) ,化简得
,化简得.files/image401.gif) 。
。
将直线.files/image391.gif) 的参数方程代入圆方程得
的参数方程代入圆方程得.files/image403.gif)
∵.files/image405.gif) ,∴
,∴.files/image407.gif) 。 …………10分
。 …………10分
24.证法一:∵.files/image409.gif) ,∴
,∴.files/image411.gif) ,又∵
,又∵.files/image413.gif) ,
,
∴.files/image415.gif) ………5分
………5分
.files/image417.gif) 。 ………10分
。 ………10分
证法二:设.files/image419.gif) =
=.files/image421.gif) ,∵
,∵.files/image409.gif) ,
,
当.files/image423.gif) 时,
时,.files/image425.gif) ;
;
当.files/image427.gif) ,
,.files/image429.gif) <0,
<0,.files/image431.gif) 是单调递减函数,………5分
是单调递减函数,………5分
∵.files/image413.gif) ,∴
,∴.files/image433.gif) ,
,
∴.files/image435.gif) =
=.files/image437.gif) =
=.files/image439.gif) ;
;
.files/image441.gif) =
=.files/image443.gif) =
=.files/image445.gif) 。
。
∴.files/image447.gif) 。
………10分
。
………10分
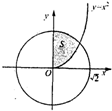 如图所示,若向圆x2+y2=2内随机投一点(该点落在圆x2+y2=2内任何一点是等可能的),则所投的点落在圆与y轴及曲线y=x2(x≥0)围成的阴影图形S内部的概率是
如图所示,若向圆x2+y2=2内随机投一点(该点落在圆x2+y2=2内任何一点是等可能的),则所投的点落在圆与y轴及曲线y=x2(x≥0)围成的阴影图形S内部的概率是
- A.
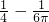
- B.
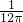
- C.

- D.
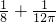
 (2009•大连二模)如图所示,若向圆x2+y2=2内随机投一点(该点落在圆x2+y2=2内任何一点是等可能的),则所投的点落在圆与y轴及曲线y=x2(x≥0)围成的阴影图形S内部的概率是( )
(2009•大连二模)如图所示,若向圆x2+y2=2内随机投一点(该点落在圆x2+y2=2内任何一点是等可能的),则所投的点落在圆与y轴及曲线y=x2(x≥0)围成的阴影图形S内部的概率是( ) 和
和 与坐标轴围成一个矩形,现向该矩形内随机投一点(该点落在矩形内任何一点是等可能的),则所投的点恰好落在曲线
与坐标轴围成一个矩形,现向该矩形内随机投一点(该点落在矩形内任何一点是等可能的),则所投的点恰好落在曲线 与
与 轴围成的区域内的概率为()
轴围成的区域内的概率为() B.
B. C.
C. D.
D.
 和
和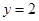 与坐标轴围成一个矩形,现向该矩形内随机投一点(该点落在矩形内任何一点是等可能的),则所投的点恰好落在曲线
与坐标轴围成一个矩形,现向该矩形内随机投一点(该点落在矩形内任何一点是等可能的),则所投的点恰好落在曲线 与
与 轴围成的区域内的概率为()
轴围成的区域内的概率为()



 和
和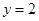 与坐标轴围成一个矩形,现向该矩形内随机投一点(该点落在矩形内任何一点是等可能的),则所投的点恰好落在曲线
与坐标轴围成一个矩形,现向该矩形内随机投一点(该点落在矩形内任何一点是等可能的),则所投的点恰好落在曲线 与
与 轴围成的区域内的概率为()
轴围成的区域内的概率为()


