摘要：又∵∴ AC∥平面GBE．----6分 (2)解:延长EG交DA的延长线于H点.连结BH.作AO⊥GH于O点.连结BO．∵ 平面ABCD⊥平面ADEF.平面ABCD∩平面ADEF＝AD .AB⊥AD∴ AB⊥平面ADEF.由三垂线定理.知AB⊥GH.故∠AOB就是二面角B-GE-D的平面角．----8分∵ 平面ABCD⊥平面ADEF.平面ABCD∩平面ADEF＝AD .ED⊥AD∴ ED⊥平面ABCD.故∠EBD就是直线BE与平面ABCD成的角.--10分
网址：http://m.1010jiajiao.com/timu_id_59571[举报]
如图，ABCD－A1B1C1D1为正方体，下面结论中正确的是_____________.
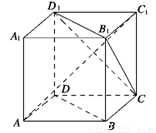① AC∥平面CB1D1；
② AC1⊥平面CB1D1；
③ AC1与底面ABCD所成角的正切值是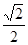
；
④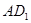 
与BD为异面直线。
查看习题详情和答案>>
（2010•昆明模拟）如图，在正方形ABCD中，E、F分别是BC、CD的中点，AC∩EF=G．现在沿AE、EF、FA把这个正方形折成一个四面体，使B、C、D三点重合，重合后的点记为P，则在四面体P-AEF中必有（ ）
查看习题详情和答案>>
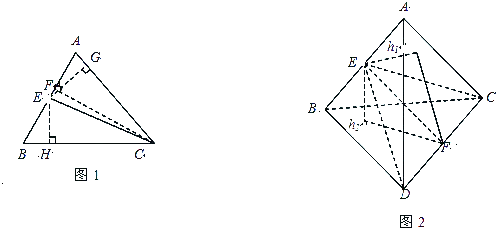
在△ABC（如图1），若CE是∠ACB的平分线，则
=
．其证明过程如下：
作EG⊥AC于点G，EH⊥BC于点H，CF⊥AB于点F，
∵CE是∠ACB的平分线，
∴EG=EH．
又∵
=
=
，
=
=
，
∴
=
（1）把上面结论推广到空间中：在四面体A-BCD中（如图2），平面CDE是二面角A-CD-B的角平分面，类比三角形中的结论，你得到的相应空间的结论是
=
=
（2）证明你所得到的结论．
查看习题详情和答案>>
| AC |
| BC |
| AE |
| BE |
作EG⊥AC于点G，EH⊥BC于点H，CF⊥AB于点F，
∵CE是∠ACB的平分线，
∴EG=EH．
又∵
| AC |
| BC |
| AC•EG |
| BC•EH |
| S△AEC |
| S△BEC |
| AE |
| BE |
| AE•CF |
| BE•CF |
| S△AEC |
| S△BEC |
∴
| AC |
| BC |
| AE |
| BE |
（1）把上面结论推广到空间中：在四面体A-BCD中（如图2），平面CDE是二面角A-CD-B的角平分面，类比三角形中的结论，你得到的相应空间的结论是
| S△ACD |
| S△BCD |
| AE |
| BE |
| S△ACD |
| S△BCD |
| AE |
| BE |
（2）证明你所得到的结论．
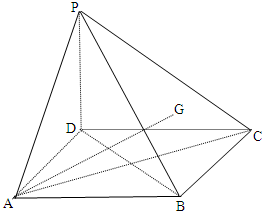如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，点G是侧面三角形PBC的重心；