摘要：20．(1)∵SA⊥平面ABCD ∴∠SDA是与平面ABCD所成角.即.∴AD=2.以A为坐标原点.AB.AD.AS为x,y,z轴建立空间直角坐标系.则
网址：http://m.1010jiajiao.com/timu_id_5936[举报]
如图，在四棱锥S-ABCD中，∠ADB=90°，AD=BD=1，SA⊥平面ABCD，∠ASB=30°，E、F分别是SD、SC上的动点，M、N分别是SB、SC上的动点，且| SE |
| SD |
| SF |
| SC |
| SM |
| SB |
| SN |
| SC |
（I）当λ，μ有何关系时，ME⊥平面SAD？并证明你的结论；
（II）在（I）的条件下且μ=
| 1 |
| 2 |
如图，四棱锥S—ABCD的底面ABCD是正方形，SA⊥平面ABCD，E是SC上一点.?
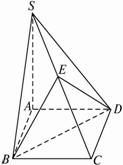
（1）求证：平面EBD⊥平面SAC；?
（2）假设SA=4，AB=2，求点A到平面SBD的距离；?
（3）当
的值为多少时，二面角B-SC-D的大小为120°?
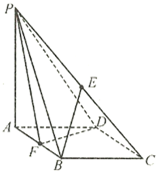如图，在四棱锥P-ABCD中，底面ABCD是菱形，∠BAD=60°，AB=2，PA=1，PA⊥平面ABCD，E是PC的中点，F是AB的中点．（1）求证：BE∥平面PDF；
（2）求证：平面PDF⊥平面PAB；
（3）求三棱锥P-DEF的体积．
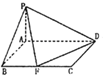如图，四边形ABCD是矩形，且AD=2，AB=1，PA⊥平面ABCD，F是线段BC的中点．
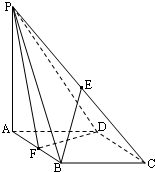（2010•武清区一模）如图在四棱锥P-ABCD中，底面ABCD是菱形，∠BAD=60°，AB=2，PA=1，PA⊥平面ABCD，E是PC的中点，F是AB的中点．