网址:http://m.1010jiajiao.com/timu_id_57295[举报]
题号
14
15
16
17
18
19
20
21
答案
A
AC
D
C
B
B
BC
CD
22.(Ⅰ) (1)甲 (2)BC (3)2.0 1.50 1.0
(Ⅱ) (1)0.25 (2)小车滑行时所受摩擦阻力较大 (3)使导轨倾斜一定的角度以平衡摩擦力
 23.解:⑴由题意可知:小球落到斜面上并沿斜面下滑,说明此时小球速度方向与斜面平行,否则小球会弹起,所以υy = υ0tan53° (2分) υy2 = 2gh
(2分)
23.解:⑴由题意可知:小球落到斜面上并沿斜面下滑,说明此时小球速度方向与斜面平行,否则小球会弹起,所以υy = υ0tan53° (2分) υy2 = 2gh
(2分)
代入数据,得υy =
⑵由υy = gt1得t1 = 0.4s (1分)
s =υ0t1 = 3×
⑶小球沿斜面做匀加速直线运动的加速度a = (1分)
初速度 =
=υt2
+ a
t22 (2分)
代入数据,整理得
4t22 + 5t2 - 26 = 0
解得 t2 =
2s 或t2 = - 13s(不合题意舍去)
(1分)
所以t =
t1 + t2 = 2.4s (1分)
24.(1)小球在C处受水平向右的电场力F和竖直向下的重力G,加速度为 g
g
则由 (3分)
(3分)
(2)从A→B由动能定理得  (3分)
(3分)  (1分)
(1分)
在B点,由牛顿运动定律得: (2分) 得
(2分) 得 (1分)
(1分)
(3) 小球从B点穿出后,在电场和重力场的复合场中做类平抛运动,由运动分解知识得:
水平方向:

 (3分)
(3分)
竖直方向: (1分) 联立解得:s=R/2
(1分) 联立解得:s=R/2  (2分)
(2分)
 由题意得: 虚线框MNPQ的高度h≥sBC+R=
由题意得: 虚线框MNPQ的高度h≥sBC+R= 宽度L≥2R (1分)
宽度L≥2R (1分)
30.A.解析:设月球表面重力加速度为g,月球质量为M.
∵球刚好完成圆周运动,∴小球在最高点有 (4分)
(4分)
从最低点至最高低点有  (4分)
(4分)
由①②可得 (3分)
(3分)
∵在月球表面发射卫星的最小速度为月球第一宇宙速度
∴ (4分)
(4分)
B.解: (1)设滑块到达B点的速度为v,由机械能守恒定律,有
 .--------4分
.--------4分
(2)滑块在传送带上做匀加速运动,受到传送带对它的滑动摩擦力,有 mg =ma,滑块对地位移为L,末速度为v0,则
mg =ma,滑块对地位移为L,末速度为v0,则 ,得
,得 --------------4分
--------------4分
(3)产生的热量等于滑块与传送带之间发生的相对位移中克服摩擦力所做的功,即
 为带与滑块间的相对位移,设所用时间为t,则
为带与滑块间的相对位移,设所用时间为t,则 , 3分
, 3分
得 。-----------4分
。-----------4分
C.解:(1)设乙物体运动到最高点时,绳子上的弹力为T1,
对乙物体  =5N
(2分)
=5N
(2分)
当乙物体运动到最低点时,绳子上的弹力为T2
对乙物体由机械能守恒定律:  (3分)
(3分)
又由牛顿第二定律: 
 (2分)
(2分)
得: =20N
(2分)
=20N
(2分)
(2)设甲物体的质量为M,所受的最大静摩擦力为f ,
乙在最高点时甲物体恰好不下滑,有: (2分)
(2分)
乙在最低点时甲物体恰好不上滑,有:  (2分)
(2分)
可解得:  (1分)
(1分)
 (1分)
(1分)
D. 解:(1)在电荷由A移到B的过程中,电势能增加了0.1J,所以电场力做功-0.1J
(2)由U=W/q,U=-0.1J/-2×10
(3)由E=U/d=U/ABCOS60O=5×105 (V/m)
A.由速度的定义v=
| ||||
| B.在探究加速度、力和质量三者之间关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系 | ||||
| C.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看做匀速直线运动,然后把各小段的位移相加 | ||||
| D.在不需要考虑物体本身的大小和形状时,用有质量的点来代替物体,即质点 |
在“探究弹性势能的表达式”的活动中,为计算弹簧弹力所做的功,把拉伸弹簧的过程分为很多小段,拉力在每小段可认为是恒力,用各小段做功的代数和代表弹力在整个过程所做的功,物理学中把这种研究方法叫做“微元法”.下面几个实例中应用到这一思想方法的是
A.由加速度的定义![]() ,当
,当![]() 非常小,
非常小,![]() 就可以表示物体在t时刻的瞬时加速度
就可以表示物体在t时刻的瞬时加速度
B.在探究加速度、力和质量三者之间的关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系![]()
C.在不需要考虑物体本身的大小和形状时,用有质量的点来代替物体,即质点
D.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加
查看习题详情和答案>>在“探究弹性势能的表达式”的活动中,为计算弹簧弹力所做的功,把拉伸弹簧的过程分为很多小段,拉力在每小段可认为是恒力,用各小段做功的代数和代表弹力在整个过程所做的功,物理学中把这种研究方法叫做“微元法”.下面几个实例中应用到这一思想方法的是
A.由加速度的定义![]() ,当
,当![]() 非常小,
非常小,![]() 就可以表示物体在t时刻的瞬时加速度
就可以表示物体在t时刻的瞬时加速度
B.在探究加速度、力和质量三者之间的关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系
C.在不需要考虑物体本身的大小和形状时,用有质量的点来代替物体,即质点
D.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加
查看习题详情和答案>>在“探究弹性势能的表达式”的活动中,为计算弹簧弹力所做的功,把拉伸弹簧的过程分为很多小段,拉力在每小段可认为是恒力,用各小段做功的代数和代表弹力在整个过程所做的功,物理学中把这种研究方法叫做“微元法”.下面几个实例中应用到这一思想方法的是
A.由加速度的定义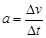 ,当 ,当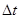 非常小, 非常小,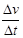 就可以表示物体在t时刻的瞬时加速度 就可以表示物体在t时刻的瞬时加速度 |
B.在探究加速度、力和质量三者之间的关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系 |
| C.在不需要考虑物体本身的大小和形状时,用有质量的点来代替物体,即质点 |
| D.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加 |