摘要：由 ①.②可知.当时...
网址：http://m.1010jiajiao.com/timu_id_567144[举报]
已知m>1，直线
，椭圆C：
，
、
分别为椭圆C的左、右焦点.
（Ⅰ）当直线过右焦点时，求直线的方程;
（Ⅱ）设直线与椭圆C交于A、B两点，△A、△B的重心分别为G、H.若原点O在以线段GH为直径的圆内，求实数m的取值范围.[
【解析】第一问中因为直线经过点（
，0），所以＝
，得
.又因为m>1，所以
，故直线的方程为
第二问中设
，由
，消去x，得
，
则由
，知
<8,且有
由题意知O为的中点.由
可知
从而
，设M是GH的中点，则M（
）.
由题意可知，2|MO|<|GH|,得到范围
查看习题详情和答案>>
甲、乙 两地相距100km，汽车从甲地匀速行驶到乙地，速度不超过60km/h，已知汽车每小时的运输成本（元）由可变部分和固定部分组成，可变部分与速度x（km/h）的平方成正比例，比例系数为
，固定部分为60元．
（Ⅰ）将全程的运输成本y（元）表示为速度x（km/h）的函数，并指出函数的定义域；
（Ⅱ）判断此函数的单调性，并求当速度为多少时，全程的运输成本最小．
查看习题详情和答案>>
| 1 | 60 |
（Ⅰ）将全程的运输成本y（元）表示为速度x（km/h）的函数，并指出函数的定义域；
（Ⅱ）判断此函数的单调性，并求当速度为多少时，全程的运输成本最小．
甲、乙 两地相距100km，汽车从甲地匀速行驶到乙地，速度不超过60km/h，已知汽车每小时的运输成本（元）由可变部分和固定部分组成，可变部分与速度x（km/h）的平方成正比例，比例系数为
，固定部分为60元．
（Ⅰ）将全程的运输成本y（元）表示为速度x（km/h）的函数，并指出函数的定义域；
（Ⅱ）判断此函数的单调性，并求当速度为多少时，全程的运输成本最小．
查看习题详情和答案>>
| 1 |
| 60 |
（Ⅰ）将全程的运输成本y（元）表示为速度x（km/h）的函数，并指出函数的定义域；
（Ⅱ）判断此函数的单调性，并求当速度为多少时，全程的运输成本最小．
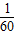，固定部分为60元．
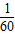，固定部分为60元．