网址:http://m.1010jiajiao.com/timu_id_5597[举报]
一、本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,有的小题只有一个选项是正确的,有的小题有多个选项是正确的。全部选对的得3分,选对但不全的得2分,有选错或不答的得0分。把你认为正确答案的代表字母填写在题后的括号内。
1.B 2.AC 3.CD 4.AB 5.D 6.CD 7.BC 8.AC 9.A 10.CD
二、本题共3小题,共14分。按照要求作图或把答案填在题中的横线上。
12.(1);(2分) ;(2分)(2)偏小。(1分)
13.(1)如答图1;(2分) (2)0~6.4;(2分)
(3)。(2分)
三、本大题包括7小题,共56分。解答应写出必要的文字说明,方程式和重要的演算步骤。
只写出最后答案的不能得分,有数值计算的题的答案必须明确写出数值和单位。
14.(7分)
解:(1)质子进入磁场做半径为R1的匀速圆周运动,洛仑滋力提供向心力,根据牛顿第二定律,…………………………(2分)
质子离开磁场时到达A点,O、A间的距离.………………(1分)
同理,α粒子在磁场中做圆周运动的半径为,α粒子离开磁场时到达B点,
O、B间的距离,则A、B两点间的距离.…(2分)
(2)α粒子在匀强磁场中运动周期为,
则α粒子在磁场中运动的时间为…………………………(2分)
15.(7分)解:(1)根据电磁感应定律,金属棒ab上产生的感应电动势为
……………………………………(1分)
根据闭合电路欧姆定律,通过R的电流……………………(1分)
金属棒两端的电压U=E-Ir=2.5V.………………………………………………(1分)
(2)由于ab杆做匀速运动,拉力和磁场对电流的安培力大小相等,即
…………………………………………………………(2分)
(3)根据焦耳定律,电阻R上消耗的电功率P=I2R=1.25W.…………………(2分)
16.(8分)解:(1)滑块沿斜面滑下的过程中,受到的滑动摩擦力,
设到达斜面底端时的速度为,根据动能定理
,…………………………(2分)
解得………………………………………………(1分)
(2)滑块第一次与挡板碰撞后沿斜面返回上升的高度最大,设此高度为,根据动能定理, ,…………………………(2分)
代入数据解得……………………………………(1分)
(3)滑块最终将静止在斜面底端,因此重力势能和电势能和减少等于克服摩擦力做的功,
即等于产生的热能,……………………(2分)
17.(8分)解:(1)因为线圈中产生的感应电流变化的周期与磁场变化的周期相同,所以由图象可知,线圈中产生交变电流的周期为T=3.14×10-2s.
所以线圈中感应电动势的最大值为……………………(2分)
(2)根据欧姆定律,电路中电流的最大值为
通过小灯泡电流的有效值为,…………………………(1分)
小灯泡消耗的电功率为P=I2R=2.88W………………………………………………(2分)
(3)在磁感应强度变化的1~1/4周期内,线圈中感应电动势的平均值
通过灯泡的平均电流……………………………………(1分)
通过灯泡的电荷量………………………………(2分)
18.(8分)解:(1)当通过金属棒的电流为I2时,金属棒在导轨上做匀加速运动,设加速度为a,根据牛顿第二定律,………………………………(1分)
设金属棒到达NQ端时的速率为,根据运动学公式,,……………(1分)
由以上两式解得:……………………………………(2分)
(2)当金属棒静止不动时,金属棒的电阻,设金属棒在导轨上运动的时间为t,
电流在金属棒中产生的热量为Q,根据焦耳定律,Q=I,…………………(2分)
根据运动学公式,,将(1)的结果代入,争得
………(2分)
19.(9分)解:(1)t=0时刻进入两板间的电子先沿OO′方向做匀速运动,即有,
而后在电场力作用下做类平抛运动,在垂直于OO′方向做匀加速运动,设到达B、D
端界面时偏离OO′的距离为y1,则.………………(2分)
t=T/2时刻进入两板间的电子先在T/2时间内做抛物线运动到达金属板的中央,而后做匀速直线运动到达金属板B、D端界面。设电子到达金属板的中央时偏离OO′的距离为y2,将此时电子的速度分解为沿OO′方向的分量与沿电场方向的分量,并设此时刻电子的速度方向与OO′的夹角为θ,电子沿直线到达金属板B、D端界面时偏离OO′的距离为,则有;
解得……………………………………………………(1分)
因此,。…………………………………………………(1分)
(2)在t=(2n+1) T/2(n=0, 1,2……)时刻进入两板间的电子在离开金属板时偏离OO′的距离最大,因此为使所有进入金属板间的电子都能够飞出金属板,应满足的条件为,解得板间电太的最大值。…………………………………………(2分)
(3)设)时刻进入两板间的电子到达荧光屏上的位置与O′点的距离为Y1;t=(2n+1)T/2(n=0,1,2……)时刻进入两板间的电子到达荧光屏上的位置与O′点的距离为,电子到达荧光屏上分布在范围内. 当满足的条件时,△Y为最大。根据题中金属板和荧光屏之间的几何关系,得到
……………………………………………………(1分)
因此电子在荧光屏上分布的最大范畴为………(2分)
20.(9分)
解:(1)粒子A在匀强磁场中做匀速圆周运动,洛仑滋力提供向心力,设粒子A的速度为v0,在MN上方运动半径为R1,运动周期为T1,根据牛顿第二定律和圆周运动公式,
解得 ………………………………(2分)
同理,粒子A在MN下方运动半径R2和周期T2分别为:
。
粒子A由P点运动到MN边界时与MN的夹角为60°,如答图2所示,则有
R1-h=R1cos60° 得到:R1=2h,R2=4h。
PQ间的距离为d=2R2sin60°-2R1sin60°=2h。………………………………(3分)
(2)粒子A从P点到Q点所用时间为
,………………………………(1分)
设粒子B的质量为M,从P点到Q点速度为v
,……………………………………………………(1分)
由
根据动量守恒定律…………(2分)
(1)小球运动通过最低点C时的速度大小;
(2)小球通过最低点C时细线对小球的拉力大小。(g取10 m/s2,sin 37°=0.6,cos 37°=0.8)

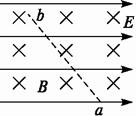
图6
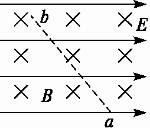
A.微粒一定带负电
B.微粒动能一定减少?
C.微粒的电势能一定增加
D.微粒的机械能一定增加?
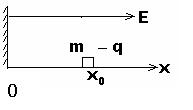
查看习题详情和答案>>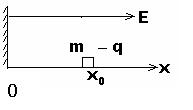 如图6所示,一质量为m、电荷量为-q的小物体,在水平轨道沿ox上运动,O端有一与轨道垂直的固定墙,轨道处在场强为E、方向沿Ox轴正向的匀强电场中,小物体以初速度υ0从x0点沿Ox轨道运动,运动中受到大小不变的摩擦力f的作用,且f<qE。设小物体与墙碰撞时的机械能损失忽略不计,则它从开始运动到停止前通过的总路程是( )
如图6所示,一质量为m、电荷量为-q的小物体,在水平轨道沿ox上运动,O端有一与轨道垂直的固定墙,轨道处在场强为E、方向沿Ox轴正向的匀强电场中,小物体以初速度υ0从x0点沿Ox轨道运动,运动中受到大小不变的摩擦力f的作用,且f<qE。设小物体与墙碰撞时的机械能损失忽略不计,则它从开始运动到停止前通过的总路程是( )![]()
A.![]() B.
B.![]()
![]()
|