网址:http://m.1010jiajiao.com/timu_id_556278[举报]
一、填空题
1. ; 2.
; 2. ;3.
;3. ; 4.
; 4. ;5. 11; 6.210; 7.16;
8.③; 9.
;5. 11; 6.210; 7.16;
8.③; 9. ; 10.
; 10. ; 11.
; 11. ; 12.
; 12. ; 13.
; 13. ; 14.
; 14. (结果为
(结果为 不扣分).
不扣分).
二、解答题
 15.(本小题满分14分)
15.(本小题满分14分)
解:(1)50;0.04;0.10. ………… 6分
(2)如图. ……………… 10分
(3)在随机抽取的 名同学中有
名同学中有 名
名
出线, . ………… 13分
. ………… 13分
答:在参加的 名中大概有63名同学出线.
名中大概有63名同学出线.
………………… 14分
16.(本小题满分14分)
解: 真,则有
真,则有 ,即
,即 . ------------------4分
. ------------------4分
 真,则有
真,则有 ,即
,即 . ----------------9分
. ----------------9分
若 、
、 中有且只有一个为真命题,则
中有且只有一个为真命题,则 、
、 一真一假.
一真一假.
①若 真、
真、 假,则
假,则 ,且
,且 ,即
,即 ≤
≤ ; ----------------11分
; ----------------11分
②若 假、
假、 真,则
真,则 ,且
,且 ,即3≤
,即3≤ . ----------------13分
. ----------------13分
故所求范围为: ≤
≤ 或3≤
或3≤ .
-----------------14分
.
-----------------14分
17.(本小题满分15分)
解:(1)设方程 有实根为事件
有实根为事件 .
.
数对 共有
共有 对.
------------------2分
对.
------------------2分
若方程有实根,则 ≥
≥ ,即
,即 . -----------------4分
. -----------------4分
则使方程有实根的数对 有
有 共
共 对.
------------------6分
对.
------------------6分
所以方程有实根的概率 .
------------------8分
.
------------------8分
(2)设方程 有实根为事件
有实根为事件 .
.
 ,所以
,所以 .
------------------10分
.
------------------10分
方程有实根对应区域为 ,
, . -------------------12分
. -------------------12分
所以方程有实根的概率 .
------------------15分
.
------------------15分
 18.(本小题满分15分)
18.(本小题满分15分)
解:(1) ∴
∴ ………………4分
………………4分
(2)过 的切线斜率
的切线斜率 .
.
∴切线方程为 .
.
准线方程为 . …………………8分
. …………………8分
∴ .∴
.∴ . ………………………………12分
. ………………………………12分
 在
在 单调递增,∴
单调递增,∴ ,
, .
.
∴ 的取值范围是-
的取值范围是- .
………………………………15分
.
………………………………15分
19.(本小题满分16分)
解:(1)设 关于l的对称点为
关于l的对称点为 ,则
,则 且
且 ,解得
,解得 ,
, ,即
,即 ,故直线
,故直线 的方程为
的方程为 .由
.由 ,解得
,解得 .
------------------------5分
.
------------------------5分
(2)因为 ,根据椭圆定义,得
,根据椭圆定义,得
 ,所以
,所以 .又
.又 ,所以
,所以 .所以椭圆
.所以椭圆 的方程为
的方程为 .
------------------------10分
.
------------------------10分
(3)假设存在两定点为 ,使得对于椭圆上任意一点
,使得对于椭圆上任意一点 (除长轴两端点)都有
(除长轴两端点)都有 (
( 为定值),即
为定值),即 ?
? ,将
,将 代入并整理得
代入并整理得 …(*).
…(*).
由题意,(*)式对任意 恒成立,所以
恒成立,所以 ,
,
解之得  或
或 .
.
所以有且只有两定点 ,使得
,使得 为定值
为定值 . ---------------16分
. ---------------16分
(注:若猜出 、
、 点为长轴两端点并求出定值,给3分)
点为长轴两端点并求出定值,给3分)
20.(本小题满分16分)
解:(1)
 .
------------------------2分
.
------------------------2分
因为 ,令
,令 得
得 ;令
;令 得
得 .所以函数的增区间为
.所以函数的增区间为 ,减区间为
,减区间为 .
------------------------5分
.
------------------------5分
(2)因为
 ,设
,设
 ,则
,则 .----------6分
.----------6分
设切点为 ,则切线的斜率为
,则切线的斜率为 ,切线方程为
,切线方程为 即
即 ,由点
,由点
 在切线上知
在切线上知 ,化简得
,化简得 ,即
,即 .
.
所以仅可作一条切线,方程是 .
------------------------9分
.
------------------------9分
(3)
 ,
, .
.
 在
在 上恒成立
上恒成立
 在
在 上的最小值
上的最小值 .--------------11分
.--------------11分
①当 时,
时, 在
在 上单调递减,
上单调递减, 在
在 上最小值为
上最小值为 ,不符合题意,故舍去;
------------------------12分
,不符合题意,故舍去;
------------------------12分
②当 时,令
时,令 得
得 .
.
当 时,即
时,即 时,函数在
时,函数在 上递增,
上递增, 的最小值为
的最小值为 ;解得
;解得 .
------------------------13分
.
------------------------13分
当 时,即
时,即 时,函数在
时,函数在 上递减,
上递减, 的最小值为
的最小值为 ,无解;
-----------------------14分
,无解;
-----------------------14分
当 时,即
时,即 时,函数在
时,函数在 上递减、在
上递减、在 上递增,所以
上递增,所以 的最小值为
的最小值为 ,无解.
------------------------15分
,无解.
------------------------15分
综上,所求 的取值范围为
的取值范围为 .
------------------------16分
.
------------------------16分
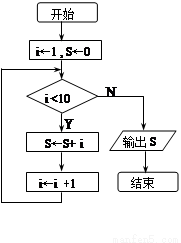
 6、一个算法的流程图如图所示,则输出的结果s为
6、一个算法的流程图如图所示,则输出的结果s为 3、一个算法的流程图如图所示,则输出S的值为
3、一个算法的流程图如图所示,则输出S的值为 一个算法的流程图如图所示,则输出的S值为
一个算法的流程图如图所示,则输出的S值为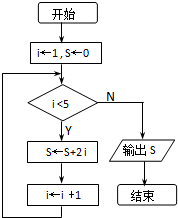 一个算法的流程图如图所示,则输出的S值为
一个算法的流程图如图所示,则输出的S值为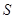 值为 .
值为 .