摘要：在具体进行构造之前.有必要了解f(x)的一些基本性质.以便构造时有正确的方向.由定义域和值域都是一切实数,如果有x1,x2使f(x1)=f(x2) .则f(f(x1))=f(f(x2)),函数的复合满足结合律.即.由此得到f+2--(2)因此.我们只要对满足0<2的实数x定义f的定义延拓到整个实数轴上即可.令为任意一个定义域和值域都为开区间(0.1)的有反函数的函数.它的反函数记为.下面k总表示整数.定义f(x)如下:
网址：http://m.1010jiajiao.com/timu_id_549685[举报]
已知函数
，
[-2，2]表示的曲线过原点，且在x＝±1处的切线斜率均为-1，有以下命题：① f(x)的解析式为：
，[-2，2]；
② f(x)的极值点有且仅有一个；
③ f(x)的最大值与最小值之和等于零；
其中正确的命题个数为（ ）
A、0个 B、1个 C、2个 D、3个
查看习题详情和答案>>
对于定义在R上的函数f(x),有下述命题:
①若f(x)为奇函数,则
的图象关于点A(1,0)对称;
②若对x∈R,有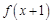
＝,则f(x)的图象关于直线x＝1对称;
③若函数的图象关于直线x＝1对称,则f(x)为偶函数;
④函数
与函数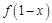
的图象关于直线x＝1对称.
其中正确命题的序号是______________.[
查看习题详情和答案>>
(文)已知函数f(x)的导数为f′(x)，若f′(x)<0(a <x <b)且f(b)>0，则在(a ，b)内必有( )
A.f(x)＝0 B.f(x)>0 C.f(x)<0 D.不能确定
查看习题详情和答案>>