摘要:用向量来证明不等式.也是方法上的创新.这两种证法都体现了学生的大胆想象力.探究精神和解题机智.一个懂得如何学习的学生在课堂上的想象力是非常丰富的.一个好的教师也应该懂得怎样来培养和保护学生的想象力.有时候.学生的想象力可能是“天马行空 .甚至是荒唐的.这时候教师还要注意引导:解题是否浪费了重要的信息?能否开辟新的解题通道?解题多走了哪些思维回路?思维.运算能否变得简洁?是否有方法的创新?能否对问题蕴涵的知识进行纵向深入地探究.梳理知识的系统性?能否加强知识的横向联系.把问题所蕴涵孤立的知识“点 扩展到系统的知识“面 ?为什么有这样的问题.它和哪些问题有联系?能否受这个问题的启发.得到一些重要的结果.有规律性的发现?能否形成独到的新见解.有自己的小发明?等等.通过不断地想象.让学生的思维能够持续飞翔.从而不断培养学生丰富的想象力.
网址:http://m.1010jiajiao.com/timu_id_549684[举报]
已知函数f(x)=
.
(1)证明:函数f(x)既是R上的奇函数,也是R上的增函数;
(2)是否存在m使f(2t2-4)+f(4m-2t)>f(0)对任意t∈[0,1]均成立?若存在,求出m的取值范围;若不存在,请说明理由.
查看习题详情和答案>>
| 2x-1 | 2x+1 |
(1)证明:函数f(x)既是R上的奇函数,也是R上的增函数;
(2)是否存在m使f(2t2-4)+f(4m-2t)>f(0)对任意t∈[0,1]均成立?若存在,求出m的取值范围;若不存在,请说明理由.
设![]() 是已知平面
是已知平面![]() 上所有向量的集合,对于映射
上所有向量的集合,对于映射![]() ,记
,记![]() 的象为
的象为![]() 。若映射
。若映射![]() 满足:对所有
满足:对所有![]() 及任意实数
及任意实数![]() 都有
都有![]() ,则
,则![]() 称为平面
称为平面![]() 上的线性变换。现有下列命题:
上的线性变换。现有下列命题:
①设![]() 是平面
是平面![]() 上的线性变换,则
上的线性变换,则![]()
②对![]() 设
设![]() ,则
,则![]() 是平面
是平面![]() 上的线性变换;
上的线性变换;
③若![]() 是平面
是平面![]() 上的单位向量,对
上的单位向量,对![]() 设
设![]() ,则
,则![]() 是平面
是平面![]() 上的线性变换;
上的线性变换;
④设![]() 是平面
是平面![]() 上的线性变换,
上的线性变换,![]() ,若
,若![]() 共线,则
共线,则![]() 也共线。
也共线。
其中真命题是 (写出所有真命题的序号)
查看习题详情和答案>>设![]() 是已知平面
是已知平面![]() 上所有向量的集合,对于映射
上所有向量的集合,对于映射![]() ,记
,记![]() 的象为
的象为![]() 。若映射
。若映射![]() 满足:对所有
满足:对所有![]() 及任意实数
及任意实数![]() 都有
都有![]() ,则
,则![]() 称为平面
称为平面![]() 上的线性变换。现有下列命题:
上的线性变换。现有下列命题:
①设![]() 是平面
是平面![]() 上的线性变换,则
上的线性变换,则![]()
②对![]() 设
设![]() ,则
,则![]() 是平面
是平面![]() 上的线性变换;
上的线性变换;
③若![]() 是平面
是平面![]() 上的单位向量,对
上的单位向量,对![]() 设
设![]() ,则
,则![]() 是平面
是平面![]() 上的线性变换;
上的线性变换;
④设![]() 是平面
是平面![]() 上的线性变换,
上的线性变换,![]() ,若
,若![]() 共线,则
共线,则![]() 也共线。
也共线。
其中真命题是 (写出所有真命题的序号)
查看习题详情和答案>>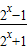 .
.