摘要:∴k≥.即k的最小值为.------------12分
网址:http://m.1010jiajiao.com/timu_id_54854[举报]
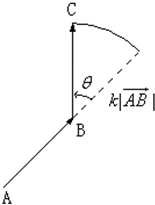 如图,
如图,| BC |
| AB |
| BC |
| AB |
| AB |
| BC |
| OA1 |
(1)向量
| OA1 |
| π |
| 2 |
| 1 |
| 2 |
| A1A2 |
| A2A3 |
| A1A2 |
| A2A3 |
(2)向量
| OA1 |
| π |
| 2 |
| 1 |
| 2 |
为
| An-1An |
| lim |
| n→∞ |
| lim |
| n→∞ |
(3)向量
| OA1 |
| A1A2 |
| A2A3 |
| OA1 |
| A1A2 |
| A2A3 |
将含有3n个正整数的集合M分成元素个数相等且两两没有公共元素的三个集合A、B、C,其中A={a1,a2,…,an},B={b1,b2,…,bn},C={c1,c2,…,cn},若A、B、C中的元素满足条件:c1<c2<…<cn,ak+bk=ck,k=1,2,…,n,则称M为“完并集合”.
(1)若M={1,x,3,4,5,6}为“完并集合”,则x的一个可能值为
(2)对于“完并集合”M={1,2,3,4,5,6,7,8,9,10,11,12},在所有符合条件的集合C中,其元素乘积最小的集合是
查看习题详情和答案>>
(1)若M={1,x,3,4,5,6}为“完并集合”,则x的一个可能值为
7,9,11
7,9,11
.(写出一个即可)(2)对于“完并集合”M={1,2,3,4,5,6,7,8,9,10,11,12},在所有符合条件的集合C中,其元素乘积最小的集合是
{6,10,11,12}
{6,10,11,12}
.