网址:http://m.1010jiajiao.com/timu_id_546682[举报]
说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.
2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数,选择题和填空题不给中间分.
一、选择题:本大题主要考查基本知识和基本运算.共10小题,每小题5分,满分50分.
题号
1
2
3
4
5
6
7
8
答案
C
A
B
A
B
C
C
D
二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,考生作答6小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题.
9. 10.
10. 11.
11. 12.
12. 
13.  14.
14. 15.2
15.2
说明:第14题答案可以有多种形式,如可答 或
或 Z
Z 等, 均给满分.
等, 均给满分.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
解:(1)∵
 ……2分
……2分
 ……4分
……4分
 .
……6分
.
……6分
∴ .
……8分
.
……8分
(2) 当 时,
时,  取得最大值, 其值为2 .
……10分
取得最大值, 其值为2 .
……10分
此时 ,即
,即
 Z
Z .
……12分
.
……12分
17.(本小题满分12分)
解:(1)设“这箱产品被用户接收”为事件 ,
, . ……3分
. ……3分
即这箱产品被用户接收的概率为 .
……4分
.
……4分
(2) 的可能取值为1,2,3.
……5分
的可能取值为1,2,3.
……5分
 =
= ,
,
 =
= ,
,
 =
= ,
……8分
,
……8分
∴ 的概率分布列为:
的概率分布列为:

1
2
3




……10分
∴ =
= .
……12分
.
……12分
18.(本小题满分14分)
解:(1)∵点A、D分别是 、
、 的中点,
的中点,
∴ .
……2分
.
……2分
∴∠ =90º.
=90º.
∴ .
.
∴  ,
,
∵ ,
,
∴ ⊥平面
⊥平面 .
……4分
.
……4分
∵ 平面
平面 ,
,
∴ .
……6分
.
……6分
(2)法1:取 的中点
的中点 ,连结
,连结 、
、 .
.
 ∵
∵ ,
,
∴ .
.
∵ ,
,
∴ 平面
平面 .
.
∵ 平面
平面 ,
,
∴ .
……8分
.
……8分
∵
∴ 平面
平面 .
.
∵ 平面
平面 ,
,
∴ .
.
∴∠ 是二面角
是二面角 的平面角.
……10分
的平面角.
……10分
在Rt△ 中,
中,  ,
,
在Rt△ 中,
中,  ,
,
 .
……12分
.
……12分
∴ 二面角 的平面角的余弦值是
的平面角的余弦值是 .
……14分
.
……14分
 法2:建立如图所示的空间直角坐标系
法2:建立如图所示的空间直角坐标系 .
.
则 (-1,0,0),
(-1,0,0), (-2,1,0),
(-2,1,0), (0,0,1).
(0,0,1).
∴ =(-1,1,0),
=(-1,1,0), =(1,0,1),
……8分
=(1,0,1),
……8分
设平面 的法向量为
的法向量为 =(x,y,z),则:
=(x,y,z),则:
 , ……10分
, ……10分
令 ,得
,得 ,
,
∴ =(1,1,-1).
=(1,1,-1).
显然, 是平面
是平面 的一个法向量,
的一个法向量, =(
=(
 ). ……12分
). ……12分
∴cos< ,
, >=
>= .
.
∴二面角 的平面角的余弦值是
的平面角的余弦值是 .
……14分
.
……14分
19. (本小题满分14分)
解:(1)依题意知, ……2分
……2分
∵ ,
,
∴ .
……4分
.
……4分
∴所求椭圆 的方程为
的方程为 .
……6分
.
……6分
(2)∵ 点
 关于直线
关于直线 的对称点为
的对称点为 ,
,
∴  ……8分
……8分
解得: ,
, .
……10分
.
……10分
∴ .
……12分
.
……12分
∵
点
 在椭圆
在椭圆 :
: 上,
上,
∴ , 则
, 则 .
.
∴ 的取值范围为
的取值范围为 .
……14分
.
……14分
20.(本小题满分14分)
解:(1)数表中前 行共有
行共有 个数,
个数,
即第i行的第一个数是 ,
……2分
,
……2分
∴ =
= .
.
∵ ,
, =2010,
=2010,
∴ i=11. ……4分
令 ,
,
解得 .
……6分
.
……6分
(2)∵

 .
……7分
.
……7分
∴ .
.
当 时,
时,  , 则
, 则 ;
;
当 时,
时,  , 则
, 则 ;
;
当 时,
时,  , 则
, 则 ;
;
当 时, 猜想:
时, 猜想:
 .
……11分
.
……11分
下面用数学归纳法证明猜想正确.
① 当 时,
时, , 即
, 即 成立;
成立;
② 假设当 时, 猜想成立,
即
时, 猜想成立,
即 ,
,
则 ,
,
∵ ,
,
∴ .
.
即当 时,猜想也正确.
时,猜想也正确.
由①、②得当 时,
时,  成立.
成立.
当 时,
时,
 .
……13分
.
……13分
综上所述, 当 时,
时,  ; 当
; 当 时,
时,
 . ……14分
. ……14分
另法( 证明当 时,
时,  可用下面的方法):
可用下面的方法):
当 时,
时,  C
C + C
+ C + C
+ C + C
+ C


 .
.
21. (本小题满分14分)
解:(1)当 时,
时, ,
,
∴
 .
.
令 =0, 得
=0, 得  .
……2分
.
……2分
当 时,
时, , 则
, 则 在
在 上单调递增;
上单调递增;
当 时,
时, , 则
, 则 在
在 上单调递减;
上单调递减;
当 时,
时, ,
,  在
在 上单调递增.
……4分
上单调递增.
……4分
∴ 当 时,
时,  取得极大值为
取得极大值为
 ;
;
当 时,
时,  取得极小值为
取得极小值为
 . ……6分
. ……6分
(2) ∵  =
=  ,
,
∴△=  =
=  .
.
① 若a≥1,则△≤0, ……7分
∴ ≥0在R上恒成立,
≥0在R上恒成立,
∴ f(x)在R上单调递增 .
∵f(0) ,
, ,
,
∴当a≥1时,函数f(x)的图象与x轴有且只有一个交点. ……9分
② 若a<1,则△>0,
∴ = 0有两个不相等的实数根,不妨设为x1,x2,(x1<x2).
= 0有两个不相等的实数根,不妨设为x1,x2,(x1<x2).
∴x1+x2 = 2,x1x2 = a.
当 变化时,
变化时, 的取值情况如下表:
的取值情况如下表:
x

x1
(x1,x2)
x2


+
0
-
0
+
f(x)
ㄊ
极大值
ㄋ
极小值
ㄊ
……11分
∵ ,
,
∴ .
.
∴
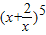 的二项展开式中,x3的系数是 (用数字作答).
的二项展开式中,x3的系数是 (用数字作答).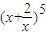 的二项展开式中,x3的系数是 (用数字作答).
的二项展开式中,x3的系数是 (用数字作答).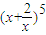 的二项展开式中,x3的系数是 (用数字作答).
的二项展开式中,x3的系数是 (用数字作答).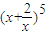 的二项展开式中,x3的系数是 (用数字作答).
的二项展开式中,x3的系数是 (用数字作答).