摘要:即与重合
网址:http://m.1010jiajiao.com/timu_id_544277[举报]
集合的表示方法
(1)确定性:即集合中的元素必须是 的,任何一个对象都能明确判断它“是”或者“不是”某个集合的元素,二者必居其一且只居其一.?
(2)互异性:集合中任意两个元素都是 的.换言之,同一个元素在一个集合里不能重复出现.?
(3)无序性:集合与它的元素的组成方式是无关的.
查看习题详情和答案>>
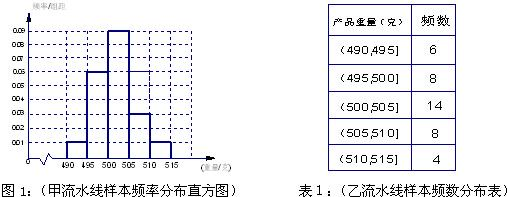
某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.

(1)根据上表数据在答题卡上作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从乙流水线上任取5件产品,恰有3件产品为合格品的概率;
(3)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为“产品的包装质量与
两条自动包装流水线的选择有关”.
附:下面的临界值表供参考:
(参考公式:K2=
,其中n=a+b+c+d)
查看习题详情和答案>>

(1)根据上表数据在答题卡上作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从乙流水线上任取5件产品,恰有3件产品为合格品的概率;
(3)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为“产品的包装质量与
两条自动包装流水线的选择有关”.
| 甲流水线 | 乙流水线 | 合计 | |
| 合格品 | a= | b= | |
| 不合格品 | c= | d= | |
| 合 计 | n= |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.图1是甲流水线样本的频率分布直方图,表1是乙流水线样本频数分布表.
(1)若以频率作为概率,试估计从甲流水线上任取5件产品,求其中合格品的件数X的数学期望;
(2)从乙流水线样本的不合格品中任意取2件,求其中超过合格品重量的件数Y的分布列;
(3)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
附:下面的临界值表供参考:
(参考公式:K2=
,其中n=a+b+c+d)
查看习题详情和答案>>

(1)若以频率作为概率,试估计从甲流水线上任取5件产品,求其中合格品的件数X的数学期望;
(2)从乙流水线样本的不合格品中任意取2件,求其中超过合格品重量的件数Y的分布列;
(3)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
| 甲流水线 | 乙流水线 | 合计 | |
| 合格品 | a= | b= | |
| 不合格品 | c= | d= | |
| 合 计 | n= |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在 的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.


表1:(甲流水线样本频数分布表) 图1:(乙流水线样本频率分布直方图)
(1)根据上表数据在答题卡上作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从两条流水线分别任取1件产品,该产品恰好是合格品的概率分别是多少;
(3)由以上统计数据完成下面 列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
|
|
甲流水线 |
乙流水线 |
合计 |
|
合格品 |
|
|
|
|
不合格品 |
|
|
|
|
合 计 |
|
|
|
附:下面的临界值表供参考:
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: ,其中
,其中 )
)
查看习题详情和答案>>
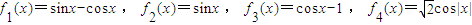 ,则它们的图象经过平移后能够重合的是函数 与函数 .(注:填上你认为正确的两个函数即可,不必考虑所有可能的情形)
,则它们的图象经过平移后能够重合的是函数 与函数 .(注:填上你认为正确的两个函数即可,不必考虑所有可能的情形)





