摘要:,即共线. ---------8分
网址:http://m.1010jiajiao.com/timu_id_542020[举报]
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
平面直角坐标系xoy中,![]() 轴上有一点A(0,1),在
轴上有一点A(0,1),在![]() 轴上任取一点P,过点P作P A的垂线
轴上任取一点P,过点P作P A的垂线![]() .
.
 (1)若
(1)若![]() 过点Q(3,2),求点P应取在何处;
过点Q(3,2),求点P应取在何处;
(2)直线![]() 能否过点R(3,3),并说明理由;
能否过点R(3,3),并说明理由;
(3)点P在![]() 轴上移动时,试确定直线
轴上移动时,试确定直线![]() 移动的区域(即直线
移动的区域(即直线![]() 可以经过的点的集合),并在给定的坐标系中用阴影部分表示出来.
可以经过的点的集合),并在给定的坐标系中用阴影部分表示出来.
如图所示的长方体 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形, 为
为 与
与 的交点,
的交点, ,
, 是线段
是线段 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角 的大小.
的大小.
【解析】本试题主要考查了线面平行的判定定理和线面垂直的判定定理,以及二面角的求解的运用。中利用 ,又
,又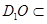 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 由
由 ,
, ,又
,又 ,∴
,∴ 平面
平面 .
可得证明
.
可得证明
(3)因为∴ 为面
为面 的法向量.∵
的法向量.∵ ,
, ,
,
∴ 为平面
为平面 的法向量.∴利用法向量的夹角公式,
的法向量.∴利用法向量的夹角公式, ,
,
∴ 与
与 的夹角为
的夹角为 ,即二面角
,即二面角 的大小为
的大小为 .
.
方法一:解:(Ⅰ)建立如图所示的空间直角坐标系.连接 ,则点
,则点 、
、 ,
,

∴ ,又点
,又点 ,
, ,∴
,∴
∴ ,且
,且 与
与 不共线,∴
不共线,∴ .
.
又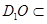 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 .…………………4分
.…………………4分
(Ⅱ)∵ ,
,
∴ ,
, ,即
,即 ,
, ,
,
又 ,∴
,∴ 平面
平面 . ………8分
. ………8分
(Ⅲ)∵ ,
, ,∴
,∴ 平面
平面 ,
,
∴ 为面
为面 的法向量.∵
的法向量.∵ ,
, ,
,
∴ 为平面
为平面 的法向量.∴
的法向量.∴ ,
,
∴ 与
与 的夹角为
的夹角为 ,即二面角
,即二面角 的大小为
的大小为
查看习题详情和答案>>